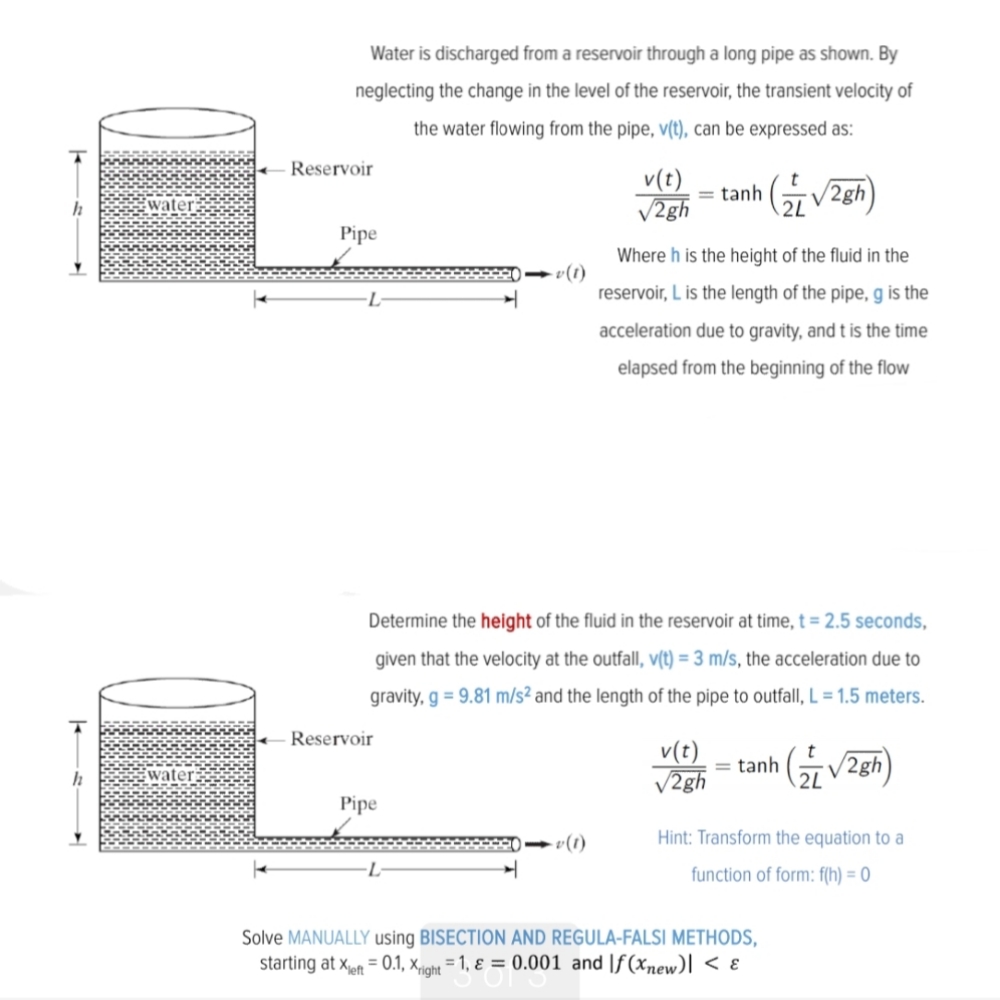
Extracted text: Water is discharged from a reservoir through a long pipe as shown. By neglecting the change in the level of the reservoir, the transient velocity of the water flowing from the pipe, v(t), can be expressed as: Reservoir v(t) V2gh = tanh 2L water Pipe Where h is the height of the fluid in the reservoir, L is the length of the pipe, g is the acceleration due to gravity, and t is the time elapsed from the beginning of the flow Determine the height of the fluid in the reservoir at time, t = 2.5 seconds, given that the velocity at the outfall, v(t) = 3 m/s, the acceleration due to gravity, g = 9.81 m/s² and the length of the pipe to outfall, L = 1.5 meters. Reservoir v(t) V2gh tanh 2L (유V2gh) water Pipe - v(1) Hint: Transform the equation to a function of form: f(h) = 0 Solve MANUALLY using BISECTION AND REGULA-FALSI METHODS, starting at xpt = 0.1, x-night = 1, ɛ = 0.001 and |f(xnew)| <>