Explain every step of the solution, especially why they used 60° rather than 30°. And how did they get R?
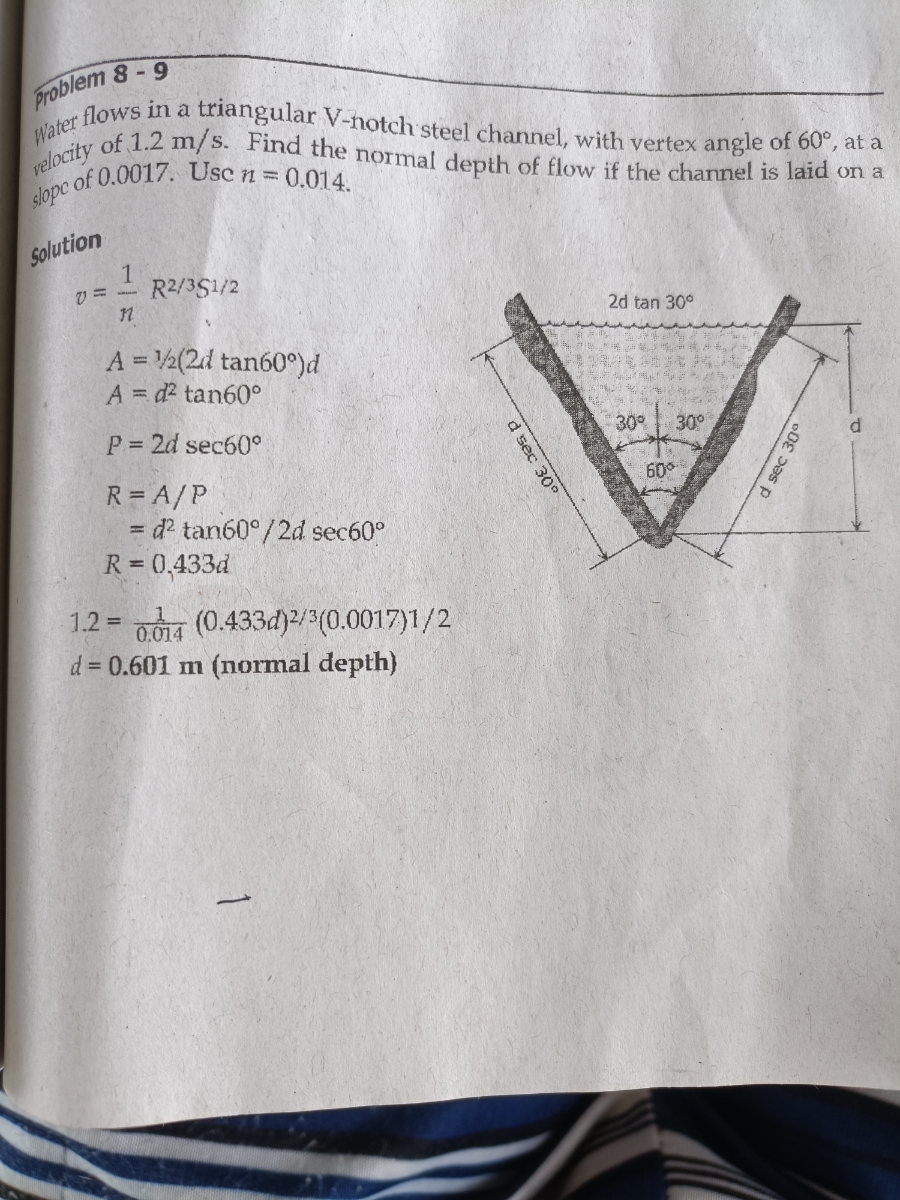
Extracted text: Water flows in a triangular V-notch steel channel, with vertex angle of 60°, at a Problem 8-9 of 1.2 m/s. Find the normal depth of flow if the channel is laid on a velocity of 0.0017. Use n 0.014. slope Solution v = - R2/351/2 2d tan 30° A = 2(2d tan60°)d A = d? tan60° P 2d sec60° 30% 30° R = A/P = d? tan60°/2d sec60° R = 0,433d 60° 001a (0.433d)/3(0.0017)1/2 d = 0.601 m (normal depth) 1.2 = d sec 30 d sec 30°