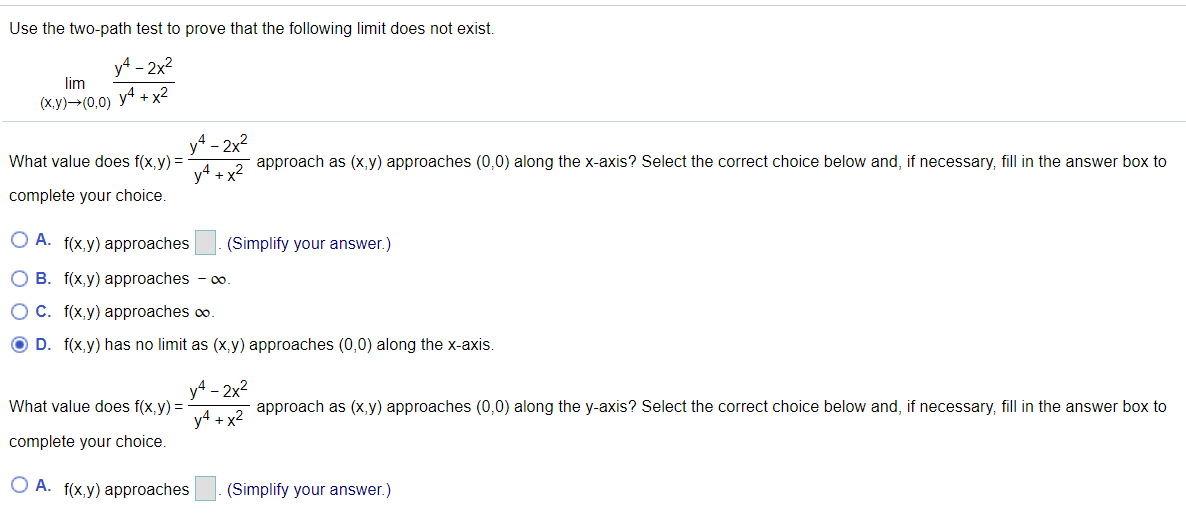
Extracted text: Use the two-path test to prove that the following limit does not exist. yA - 2x2 lim (х,у)— (0,0) у4 + x2 yA - 2x? y4 + x2 What value does f(x,y) = approach as (x, y) approaches (0,0) along the x-axis? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. f(x,y) approaches (Simplify your answer.) O B. f(x,y) approaches - 0o. OC. f(x,y) approaches co. O D. f(x,y) has no limit as (x,y) approaches (0,0) along the x-axis. y4 - 2x2 What value does f(x,y) = approach as (x,y) approaches (0,0) along the y-axis? Select the correct choice below and, if necessary, fill in the answer box to y4 + x2 complete your choice. O A. f(x,y) approaches (Simplify your answer.)

Extracted text: y4 – 2x2 What value does f(x,y) = approach as (x, y) approaches (0,0) along the y-axis? Select the correct choice below and, if necessary, fill in the answer box to y4 + x2 complete your choice. O A. f(x,y) approaches (Simplify your answer.) O B. f(x,y) approaches co. O C. f(x,y) approaches - o. O D. f(x,y) has no limit as (x,y) approaches (0,0) along the y-axis. Why does the given limit not exist? O A. As (x,y) approaches (0,0) along different paths, f(x,y) approaches two different values. O B. As (x,y) approaches (0,0) along different paths, f(x,y) always approaches the same value. OC. As (x,y) approaches (0,0) along different paths, f(x,y) does not always approach a finite value.