Two pipes (L 1 = 2.5 m and L 2 = 1.5 m) are joined at B by flange plates (thickness t f = 14 mm) with five bolts (d bf = 13 mm) arranged in a circular pattern (see figure). Also, each pipe segment is...

Two pipes (L₁
= 2.5 m and L₂
= 1.5 m) are joined at B by flange plates (thickness t_f
= 14 mm) with five bolts (d_bf
= 13 mm) arranged in a circular pattern (see figure). Also, each pipe segment is attached to a wall (at A and C, see figure) using a base plate (t_b
= mm) and four bolts (d_bb
= 16 mm). All bolts are tightened until just snug. Assume E₁
= 110 GPa, E₂
=73 GPa, v₁
= 0.33, and v₂
=  0.25. Neglect the self-weight of the pipes, and assume the pipes are in a stress-free state initially. The crosssectional areas of the pipes are A₁
= 1500 mm²
and A₂
= (3/ 5)A₁. The outer diameter of Pipe 1 is 60 mm. The outer diameter of Pipe 2 is equal to the inner diameter of Pipe 1. The bolt radius r = 64 mm for both base and flange plates.

(a) If torque T is applied at x = L₁, find an expression for reactive torques R₁
and R₂
in terms of T.

(b) Find the maximum load variable T (i.e., T_max) if allowable torsional stress in the two pipes is t_allow
= 65 MPa.

(c) Draw torsional moment (TMD) and torsional displacement (TDD) diagrams. Label all key ordinates. What is

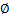
_max?

(d) Find T_max
if allowable shear and bearing stresses in the base plate and flange bolts cannot be exceeded. Assume allowable stresses in shear and bearing for all bolts are T_allow
=45 MPa and

_allow
=90 MPa.

(e) Remove torque T at x = L₁. Now assume the flange-plate bolt holes are misaligned by some angle β (see figure). Find the expressions for reactive torques R₁
and R₂
if the pipes are twisted to align the flange-plate bolt holes, bolts are then inserted, and the pipes released.

(f) What is the maximum permissible misalignment angle

_max
if allowable stresses in shear and bearing for all bolts [from part (d)] are not to be exceeded?