Two machines are used for filling plastic bottles with a net volume of 16.0 ounces. The fill volume can be assumed normal, with standard deviation σ1 = 0.020 and σ2 = 0.025 ounces. A member of the quality engineering staff suspects that both machines fill to the same mean net volume, whether or not this volume is 16.0 ounces. A random sample of 10 bottles is taken from the output of each machine. (see the table attached) MACHINE 1 MACHINE 2 16.03 16.01 16.02 16.03 16.04 15.96 15.97 16.04 16.05 15.98 15.96 16.02 16.05 16.02 16.01 16.01 16.02 15.99 15.99 16.00 (a) Do you think the engineer is correct? Use α = 0.05. (b) What is the P-value for this test? (c) What is the power of the test in part (a) for a true difference in means of 0.04? (d) Find a 95% confidence interval on the difference in means. Provide a practical interpretation of this interval. (e) Assuming equal sample sizes, what sample size should be used to assure that β = 0.05 if the true difference in means is 0.04? Assume that α = 0.05.
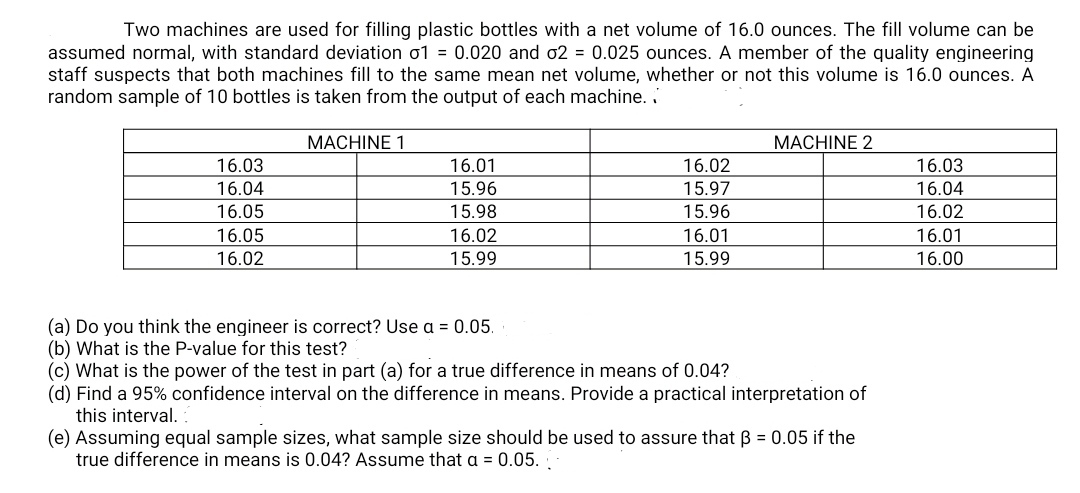
Extracted text: Two machines are used for filling plastic bottles with a net volume of 16.0 ounces. The fill volume can be assumed normal, with standard deviation o1 = 0.020 and o2 = 0.025 ounces. A member of the quality engineering staff suspects that both machines fill to the same mean net volume, whether or not this volume is 16.0 ounces. A random sample of 10 bottles is taken from the output of each machine. MACHINE 1 MACHINE 2 16.03 16.01 16.02 16.03 16.04 15.96 15.97 16.04 16.05 15.98 15.96 16.02 16.05 16.02 16.01 16.01 16.02 15.99 15.99 16.00 (a) Do you think the engineer is correct? Use a = 0.05. (b) What is the P-value for this test? (c) What is the power of the test in part (a) for a true difference in means of 0.04? (d) Find a 95% confidence interval on the difference in means. Provide a practical interpretation of this interval. (e) Assuming equal sample sizes, what sample size should be used to assure that B = 0.05 if the true difference in means is 0.04? Assume that a = 0.05.