This problem considers the following
×
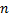
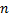
tri-diagonal matrix:
It is assumed that
> 0 and
≥ 3.
(a) Assuming
=
, the eigenvalues of
A
are λ
i
=
+ 2|| cos(
), for
= 1, 2,...,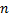, where
=
/(
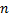
+ 1). Show that
is an eigenvector for λ
i
, where
=
.
(b) The matrix in part (a) is symmetric. Explain why it is positive definite if
≥ 2||.
(c) For the eigenvectors in part (a), show that
x
i
x
j
= 0 if
, and
x
i
x
i
= (
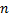
+ 1)/2.
(d) The eigenvalues of
A
are λ
i
= a + 2
cos(), for
= 1, 2,...,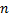, where
=
/(
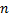
+ 1). Show that
is an eigenvector for λ
i
, where
=
and
=
.