This problem concerns the configuration shown in Figure 2.21. There are four straight sides, of fixed length, that are free to rotate at the vertices. The bottom side, of length
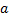, does not move. What is of interest is how the angle
changes as
changes. This is a situation that arises in kinematics, and it has been found that the two angles are related through the equation
where
=
/
,
=
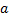, and
= (
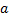
2
+
2
−
2
+
2)/(
). In textbooks on the kinematics of machines this is known as the Freudenstein equation.
(a) If θ = 0 then a triangle is produced. In this case, using the law of cosines, find ϕ and show that this is the same result obtained from (2.29). In the rest of the problem let
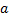= 3/2,
=
,
= 1, and
= 1/2.
(b) Taking
= 0, plot the left and right hand sides of (2.29) for 0 ≤
≤ 2
and show that there are two solutions. Explain geometrically why there are two, and identify which one corresponds to the configuration shown in Figure 2.21.
(c) Assuming Newton’s method is used to find ϕ, what is (2.10) when applied to (2.29)? Use this to calculate ϕ for
=
/6 and
=
/3. Your values should be correct to six significant digits.
(d) As θ increases from
= 0 to
= 2, the vertex connecting side
and
traces out a portion of a circle. Explain why, and find the maximum and minimum values of ϕ that determine this circular arc.