This exercise explores some of the differences between a cubic polynomial and a cubic spline. In this problem the data are: ( 1 , 1 ) = (0, 0), ( 2 , 2 ) = (1, 1), ( 3 , 3 ) = (2, 0), and ( 4 , 4 ) =...

This exercise explores some of the differences between a cubic polynomial and a cubic spline. In this problem the data are: (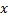
₁,

₁) = (0, 0), (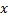
₂,

₂) = (1, 1), (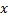
₃,

₃) = (2, 0), and (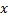
₄,

₄) = (3, 1).

(a) Find the global interpolation polynomial that fits this data, and then evaluate this function at
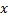 = 1/2.

(b) Find the natural cubic spline that fits this data, and then evaluate this function at
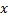 = 1/2.

(c) The cubic in part (a) satisfies the interpolation and smoothness conditions required of a spline, yet it produces a different result than the cubic spline in part (b). Why?

(d) What boundary conditions should be used so the cubic spline produces the cubic in part (a)?