This exercise concerns an implicitly defined function
(
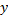), defined through an equation of the form
(,
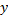) = 0. For the equations in Table 2.9, select one and then do the following:
(a) Sketch the functions as a function of
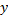, and use this to show that for each
, there is one solution
.
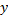(b) Use the sketch in part (a) to find a bounded interval for
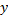that contains the solution (note the interval will possibly depend on
).
(c) What is Newton’s iteration formula (2.10) for this equation? Also, provide a starting point
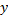
0
for the solution, providing an explanation of why it is a good choice.
(d) What is the secant iteration formula (2.24) for this equation? Also, provide starting points
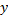
0
and
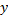
1
for the solution, providing an explanation of why they are a good choice.
(e) Compute
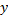(2). Your answer should be correct to at least four significant digits. Make sure to state which numerical method was used, why you made this choice, and what error condition you used to stop the calculation.
(f) Plot
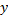() for 2 ≤
≤ 10. You should also provide an explanation of the algorithm you used to do this.