The terminal velocity
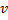
of a sphere falling through the air satisfies

where

=

2/4. In this expression,

is the density of air,

and

are the mass and diameter of the sphere, and

is the gravitational acceleration constant. The term

D
is known as the drag coefficient, and from experimental data the following formula has been proposed [White, 2005]:

where

=

is known as the Reynolds number and

is the (dynamic) viscosity of air. In this problem, (2.32) is rewritten in terms of
 , and it is then solved for
, and it is then solved for
 . After this, the value of
. After this, the value of
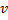
is computed. Also, note that the velocity is positive.
(a) Show that it is possible to rewrite (2.32) as ( )2
)2

D
=
 , where
, where

does not depend on
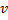
or
 . After substituting (2.33) into this equation, the problem is rewritten so
. After substituting (2.33) into this equation, the problem is rewritten so

is the variable to solve for. Write down the resulting equation. Assuming the value of

has been computed, explain how the velocity is calculated.
(b) Write the equation in part (a) as

D

=
 , where
, where

D
is given in (2.33). Sketch the left and right hand sides of this equation as a function of
 . From this show that there is one solution and it is in the interval 0
. From this show that there is one solution and it is in the interval 0

 /24.
/24.
(c) Assuming Newton’s method is used to find
 , what is (2.10) when applied to the equation in part (a)? Based on your results from part (b), what would be a good choice for a starting point? Make sure to explain why.
, what is (2.10) when applied to the equation in part (a)? Based on your results from part (b), what would be a good choice for a starting point? Make sure to explain why.
(d) Write down the iteration formula if the secant method is used to find
 . Based on your results from part (b), what would be a good choice for the two starting points? Make sure to explain why.
. Based on your results from part (b), what would be a good choice for the two starting points? Make sure to explain why.
(e) For air,

= 1.8 × 10−5,
= 1.2,

= 9.8, and for a baseball,

= 0.075 and

= 0.14 (using
 ,
,

units). What is the terminal velocity of a baseball (assuming it is a perfect sphere)? Make sure to state which method was used, why you made this choice, and what error condition you used to stop the calculation. Also, how does this velocity compare to what is considered the velocity of a typical fastball in professional baseball?
(f) Is it possible to make a baseball out of something so its terminal velocity is approximately the speed of sound?