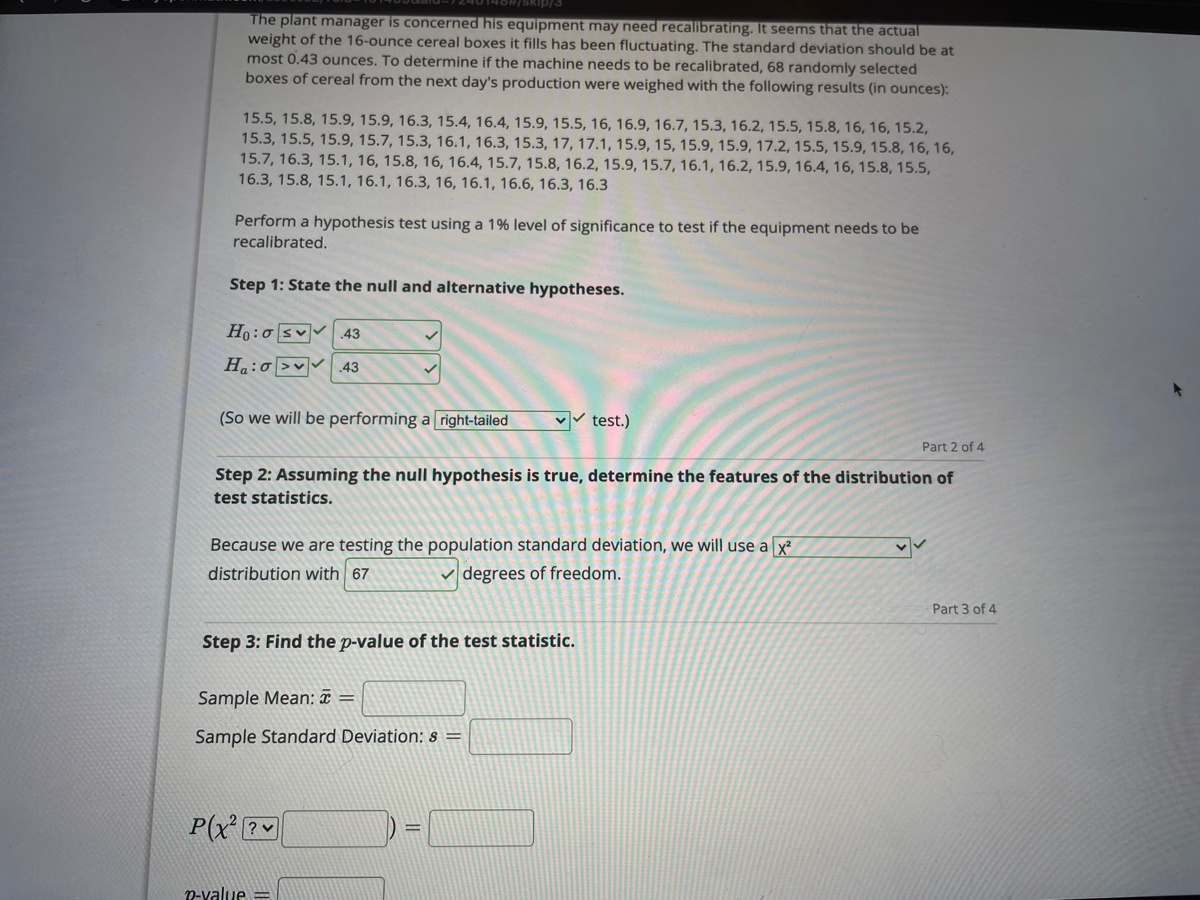
Extracted text: The plant manager is concerned his equipment may need recallibrating. It seems that the actual weight of the 16-ounce cereal boxes it fills has been fluctuating. The standard deviation should be at most 0.43 ounces. To determine if the machine needs to be recalibrated, 68 randomly selected boxes of cereal from the next day's production were weighed with the following results (in ounces): 15.5, 15.8, 15.9, 15.9, 16.3, 15.4, 16.4, 15.9, 15.5, 16, 16.9, 16.7, 15.3, 16.2, 15.5, 15.8, 16, 16, 15.2, 15.3, 15.5, 15.9, 15.7, 15.3, 16.1, 16.3, 15.3, 17, 17.1, 15.9, 15, 15.9, 15.9, 17.2, 15.5, 15.9, 15.8, 16, 16, 15.7, 16.3, 15.1, 16, 15.8, 16, 16.4, 15.7, 15.8, 16.2, 15.9, 15.7, 16.1, 16.2, 15.9, 16.4, 16, 15.8, 15.5, 16.3, 15.8, 15.1, 16.1, 16.3, 16, 16.1, 16.6, 16.3, 16.3 Perform a hypothesis test using a 1% level of significance to test if the equipment needs to be recalibrated. Step 1: State the null and alternative hypotheses. Ho:o sv 43 H:o >v 43 (So we will be performing a right-tailed v test.) Part 2 of 4 Step 2: Assuming the null hypothesis is true, determine the features of the distribution of test statistics. Because we are testing the population standard deviation, we will use a x? distribution with 67 degrees of freedom. Part 3 of 4 Step 3: Find the p-value of the test statistic. Sample Mean: ¤ = Sample Standard Deviation: s = P(x ? n-value