The ideal gas law states that
=
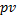
, where
is the pressure,
is the volume,
is the amount of the substance (in moles),
is the gas constant, and
is the temperature (in Kelvin). An improved version of this is the van der Waals equation of state, and it is given as
where
and
are positive constants. Also,
and
are positive.
(a) Explain why there is one solution for
. Note, one way to do this is to rewrite (2.34) as
+
2
/
2
=
/(
), and then sketch the left and right hand sides as functions of
.
(b) Using the sketch from part (a), explain why the solution satisfies
+
/.
(c) Assuming Newton’s method is used to find
, what is (2.10) when applied to (2.34)? Based on parts (a) and (b), what would be a good choice for a starting point? Make sure to explain why.
(d) Write down the iteration formula if the secant method is used to find
. Based on parts (a) and (b), what would be a good choice for the two starting points? Make sure to explain why.
(e) Assume that
= 1 atm,
= 1 mol, and recall that
= 0.08205746 L atm/(K mol). Also, for oxygen, which is the gas considered here,
= 1.382 and
= 0.0319. Note that the values for
,
and
are the exact values given in the 2012 CRC Handbook of Chemistry and Physics. Using either (c) or (d), determine
at room temperature (you can assume this is 25◦ C). In your write-up, state why you picked the solver you used, and give your reason(s) for what value you selected for the error tolerance used to stop the solver. Also, explain why it isn’t necessary to run the solver to the point that the error in the solution is on the order of machine
.
(f) Using the values given in part (e), plot
as a function of
, for 0◦
≤
≤ 50◦. In your write-up explain how you used your solver to do this.