The following (X’X)−1,
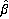 , and residual sum of squares were obtained from the regression of plant dry weight (grams) from n = 7 experimental fields on percent soil organic matter (X1) and kilograms of supplemental nitrogen per 1000 m2
, and residual sum of squares were obtained from the regression of plant dry weight (grams) from n = 7 experimental fields on percent soil organic matter (X1) and kilograms of supplemental nitrogen per 1000 m2
(X2). The regression model included an intercept.
(a) Give the regression equation and interpret each regression coefficient. Give the units of measure of each regression coefficient.
(b) How many degrees of freedom does SS(Res) have? Compute s2, the variance of
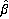
1, and the covariance of
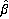
1
and
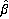
2.
(c) Determine the 95% univariate confidence interval estimates of β1
and β2. Compute the Bonferroni and the Scheff´e confidence intervals for β1
and β2
using a joint confidence coefficient of .95.
(d) Suppose previous experience has led you to believe that one percentage point increase in organic matter is equivalent to .5 kilogram/1,000 m2
of supplemental nitrogen in dry matter production. Translate this statement into a null hypothesis on the regression coefficients. Use a t-test to test this null hypothesis against the alternative hypothesis that supplemental nitrogen is more effective than this statement would imply.
(e) Define K and m for the general linear hypothesis H0: Kβ
− m = 0 for testing H0: 2β1
= β2. Compute Q and complete the test of significance using the F-test. What is the alternative hypothesis for this test?
(f) Give the reduced model you obtain if you impose the null hypothesis in (e) on the model. Suppose this reduced model gave a SS(Res) = 164.3325. Use this result to complete the test of the hypothesis.