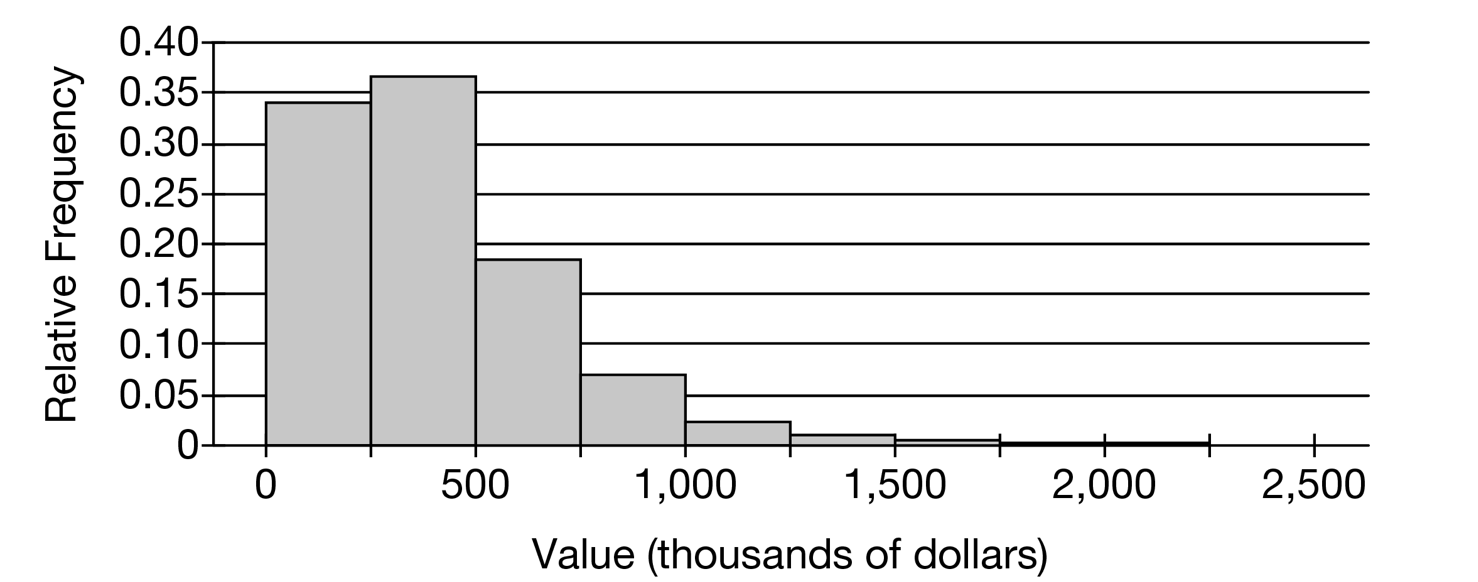
The following histogram shows the distribution of house values in a certain city. The mean of the distribution is $403,000 and the standard deviation is $278,000.
(a) Suppose one house from the city will be selected at random. Use the histogram to estimate the probability that the selected house is valued at less than $500,000. Show your work.
(b) Suppose a random sample of 40 houses are selected from the city. Estimate the probability that the mean value of the 40 houses is less than $500,000. Show your work.
To estimate a population mean μ, the sample mean x¯ is often used as an estimator. However, a different estimator is called the sample midrange, given by the formula sample minimum + sample maximum2.
(c) The following table shows the values, in thousands of dollars, of 40 randomly selected houses in the city.
| 34 | 38 | 95 | 110 | 137 | 140 | 155 | 155 | 169 | 207 |
| 209 | 217 | 274 | 314 | 314 | 323 | 343 | 347 | 349 | 363 |
| 369 | 373 | 388 | 389 | 397 | 416 | 448 | 450 | 483 | 487 |
| 488 | 516 | 571 | 595 | 600 | 738 | 762 | 769 | 863 | 1,084 |
(i) Calculate the sample midrange for the data.
(ii) Explain why the sample midrange might be preferred to the sample mean as an estimator of the population mean.
(d) To investigate the sampling distribution of the sample midrange, a simulation is performed in which 100 random samples of size n=40 were selected from the population of house values. For each sample, the sample midrange was calculated and recorded on the following dotplot. The mean of the distribution of sample midranges is $617,000 with standard deviation $136,000.
Based on the results of the simulation, explain why the sample mean might be preferred to the sample midrange as an estimator of the population mean.
Extracted text: 0.40- 0.35- 0.30- 0.25- 0.20- 0.15 0.10- 0.05- 500 1,000 1,500 2,000 2,500 Value (thousands of dollars) Relative Frequency

Extracted text: :...! 400 500 600 700 800 900 1,000 1,100 Sample Midrange (thousands of dollars)