The exercises that I am struggling with are 11 and 12 but since exercise 11 depends on 10, I'm going to add exercise 10 but you don't need to answer exercise 10. I Just need 11 and 12. thank you very...

The exercises that I am struggling with are 11 and 12 but since exercise 11 depends on 10, I'm going to add exercise 10 but you don't need to answer exercise 10.  I Just need 11 and 12. thank you very much.

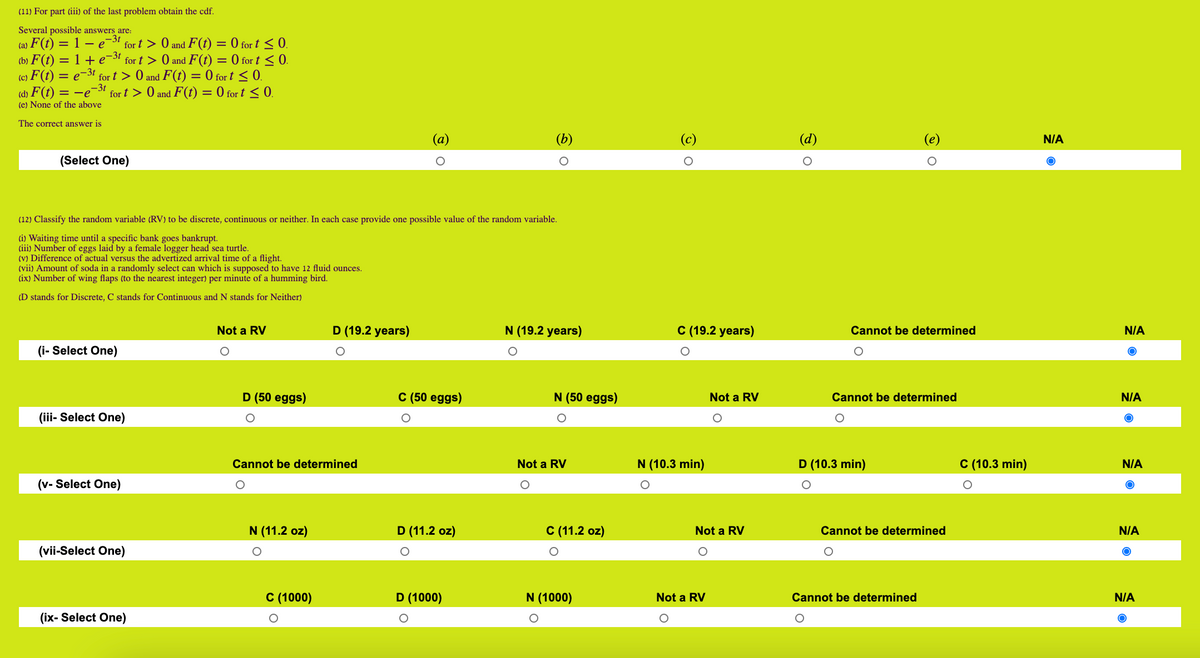
Extracted text: (11) For part (iii) of the last problem obtain the cdf. Several possible answers are: –3t (b) F(t) = 1 + e-3t (c) F (t) (a) F(t) = 1 – e-3 for t > 0 and F(t) = 0 for t <0. for="" t=""> 0 and F(t) = 0 for t < 0.="" f(t)="0" for="" t="">< 0.="" (d)="" f(t)="-e-3!" for="" t=""> 0 and F(t) = 0 for t < 0.="" %3d="" e-3t="" for="" t=""> 0 and %3D (e) None of the above The correct answer is (а) (b) (c) (d) N/A (Select One) (12) Classify the random variable (RV) to be discrete, continuous or neither. In each case provide one possible value of the random variable. (i) Waiting time until a specific bank goes bankrupt. (iii) Number of eggs laid by a female logger head sea turtle. (V) Difference of actual versus the advertized arrival time of a flight. (vii) Amount of soda in a randomly select can which is supposed to have 12 fluid ounces. (ix) Number of wing flaps (to the nearest integer) per minute of a humming bird. (D stands for Discrete, C stands for Continuous and N stands for Neither) Not a RV D (19.2 years) N (19.2 years) C (19.2 years) Cannot be determined N/A (i- Select One) D (50 eggs) C (50 eggs) N (50 eggs) Not a RV Cannot be determined N/A (iii- Select One) Cannot be determined Not a RV N (10.3 min) D (10.3 min) C (10.3 min) N/A (v- Select One) N (11.2 oz) D (11.2 oz) С (11.2 оz) Not a RV Cannot be determined N/A (vii-Select One) C (1000) D (1000) N (1000) Not a RV Cannot be determined N/A (ix- Select One)


Extracted text: (10) Find the constant C > 0 so that the given function is a density of some continuous random variable X. 3D сх, оn [0, 1], [О, оо). of(x) = (ii f (x) = ce-3x , on [1, c0), (vii f (x) = cxe*, on [O, ∞), (ix) f (x) = c sin x, on (mf(x) = c/x³ , on (0, t), 1 N/A (Select One for (i)) 3 -1 2 N/A (Select One for (iii)) 1 2 3 4 N/A (Select One for (v) -1 -2 2 N/A (Select One for (vii)) 2 1/2 a/2 N/A (Select One for (ix)) (11) For part (iii) of the last problem obtain the cdf. Several possible answers are: (a) F(t) = 1 – e-3t for t > 0 and F(t) = 0 for t < 0.="" (b)="" f(t)="1" +="" e-3t="" (c)="" f(t)="e-31" for="" t=""> 0 and F(t) = 0 for t < 0.="" (d)="" f(t)="-e-31" for="" t=""> 0 and F(t) = 0 for t < 0.="" (e)="" none="" of="" the="" above="" for="" t=""> 0 and F(t) = 0 for t < 0. –3t the correct answer is (a) (d) (e) n/a (select one) -in o 3. - o 2. 0.="" –3t="" the="" correct="" answer="" is="" (a)="" (d)="" (e)="" n/a="" (select="" one)="" -in="" o="" 3.="" -="" o="">