The equation for a string on an elastic foundation is
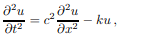
where

and

are positive constants. The problem for finding the natural frequencies of the string can be reduced to solving
Ax
= λx, where
Note that
A
is an

×

symmetric tri-diagonal matrix, and

Also, by solving the string equation one finds that the exact values for the λ’s are
(a) Explain why
A
is positive definite.
(b) Use inverse orthogonal iteration to compute the five smallest eigenvalues of
A. To do this take

= 250 and

=

= 1. Also, compute the relative error as in Table 4.16.
(c) The exact eigenvalues of
A
are λ
i
=

+ 2 cos( ), for
), for

= 1, 2,..., , where
, where

=
 /(
/(
+ 1). Taking
= 250 and

=

= 1, as in Figure 4.4, plot the ratios λ
i
−1/λ
i
and use this to explain why inverse orthogonal iteration should converge relatively quickly when computing the smaller eigenvalues.