The effect of supplemental ascorbate, vitamin C, on survival time of terminal cancer patients was studied. [Data are from Cameron and Pauling (1978) as reported in Andrews and Herzberg (1985).] The
survival time (Days) of each treated patient was compared to the mean survival time of a control group (Cont.) of 10 similar patients. Age of patient was also recorded. For this exercise, the results are used from three cancer types—stomach, bronchus, and colon. There were 13, 17, and 17 patients in the three groups, respectively. For this question use the logarithm of the ratio of days survival of the treated patient to the mean days survival of his or her control group as the dependent variable.
(a) Use the means model reparameterization to compute the analysis of variance for ln(survival ratio). Determine X∗
X∗, X∗
Y, β∗, SS(Model), SS(Res), and s2. What is the least squares estimate of the mean ln(survival ratio) for each cancer group and what is the standard error of each mean? Two different kinds of hypotheses are of interest: does the treatment increase survival time; that is, is ln(survival ratio) significantly greater than zero for each type cancer; and are there significant differences among the cancer types in the effect of the treatment? Use a t-test to test the null hypothesis that the true mean ln(survival ratio) for each group is zero. Use an F-test to test the significance of differences among cancer types.
(b) The ages of the patients in the study varied from 38 to 79; the mean age was 64.3191 years. Augment the X∗
matrix in Part (a) with the vector of centered ages. Compute the residual sum of squares and the estimate of σ2 for this model. Compute the standard error of each estimated regression coefficient. Use a t-test to test the null hypothesis that the partial regression coefficient for the regression of ln(survival ratio) on age is zero. Use the difference in residual sums of squares between this model and the previous model to test the same null hypothesis. How are these two tests related? What is your conclusion about the importance of adjusting for age differences?
(c) Since the means model was used in Part (b) and ages were expressed as deviations from the mean age, the first three regression coefficients in β are the estimates of the cancer group means adjusted to the mean age of 64.3191. Construct K for the hypothesis that the true means, adjusted for age differences, of the stomach and bronchus cancer groups, the first and second groups, are the same as for colon cancer, the third group. Complete the test and state your conclusion.
(d) Describe how X∗
c would be defined to adjust all observations to age 60 for all patients. Show the form of T for averaging the adjusted observations to obtain the adjusted group means. The adjusted group means are obtained as T X∗
cβ∗. Compute T X∗
c and s2(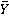
adj) for this example.
(e) Even though the average regression on age did not appear important, it was decided that each cancer group should be allowed to have its own regression on age to verify that age was not important in any of the three groups. Illustrate how X∗ would be expanded to accomodate this model and complete the test of the null hypothesis that the regressions on age are the same for all three cancer groups. State your conclusion. 9