how to solve I1,I2,I3,I4?
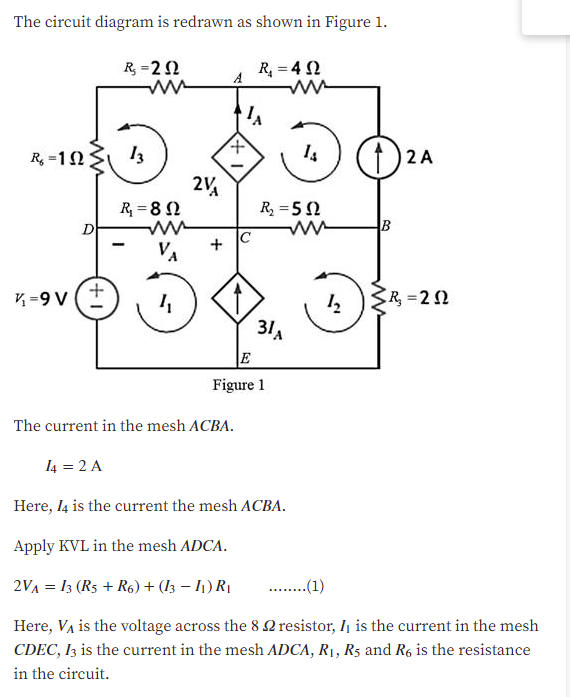
Extracted text: The circuit diagram is redrawn as shown in Figure 1. R, =2 2 R, = 4 2 t, R =1N3 13 (f) 2A 2V R = 8 2 R =5 N D |C VA K =9 V SR, =2 2 31. E Figure 1 The current in the mesh ACBA. I4 = 2 A Here, 4 is the current the mesh ACBA. Apply KVL in the mesh ADCA. 2VA = 13 (R5 + R6) + (I3 – I1) R1 .(1) Here, Va is the voltage across the 8 2 resistor, Ij is the current in the mesh CDEC, I3 is the current in the mesh ADCA, R1, R5 and R6 is the resistance in the circuit. +,

Extracted text: Simplify further. -811 – 712 + 813 =-1 A .(2) The expression for the current in the branch CE can be written as. 31A = I1 – h ..(3) The expression for the current in the branch AC. IA = 13 – 14 Substitute 2 A for l4 in the above equation. IA = 13 – 2 A Substitute l3 – 2 A for Ia in equation (3). 3 (13 – 2 A) = I1 – 2 313 – 6 A = I1 – h Simplify further. I1 - 2 – 313 = -6 A -(4) Equate equation (1), (2) and (4) for I1, 12 and I3. The value of the current I is 3.804 A, I2 is –0.340 A and I3 is 3.381 A. Conclusion: Thus, the mesh currents are Ij is 3.804 A, I2 is –0.340 A, I3 is 3.381 A and I4 is 2 A.