The Acme Company is trying to decide whether to market a new product. As in many new-product situations, there is considerable uncertainty about whether the new product will eventually be popular. Acme believes that it might be wise to introduce the product in a regional test market before introducing it nationally. Therefore, the company’s first decision is whether to conduct the test market.
Acme estimates that the net cost of the test market is $100,000. We assume this is mostly fixed costs, so that the same cost is incurred regardless of the test market results. If Acme decides to conduct the test market, it must then wait for the results. Based on the results of the test market, it can then decide whether to market the product nationally, in which case it will incur a fixed cost of $7 million. On the other hand, if the original decision is not to run a test market, then the final decision—whether to market the product nationally—can be made without further delay. Acme’s unit margin, the difference between its selling price and its unit variable cost, is $18. We assume this is relevant only for the national market.
Acme classifies the results in either the test market or the national market as great, fair, or awful. Each of these results in the national market is accompanied by a forecast of total units sold. These sales volumes (in 1000s of units) are 600 (great), 300 (fair), and 90 (awful). In the absence of any test market information, Acme estimates that probabilities of the three national market outcomes are 0.45, 0.35, and 0.20, respectively. In addition, Acme has the following historical data from products that were introduced into both test markets and national markets:
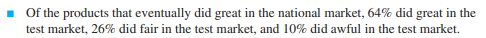

The company wants to use a decision tree approach to find the best strategy. It also wants to find the expected value of the information provided by the test market.
Objective To develop a decision tree to find the best strategy for Acme, to perform a sensitivity analysis on the results, and to find EVSI and EVPI.