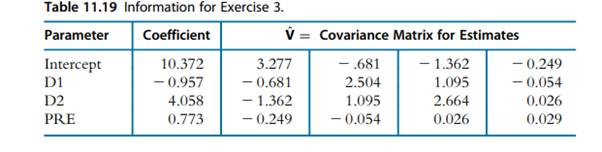
Table 11.19 gives the parameter estimates and their covariance matrix for the analysis of POST-course math scores from Example 11.3, with PRE used as a covariate. Dummy variables for CLASS used reference cell coding with
CLASS = 1 as the baseline group:
D1 = 1 if CLASS = 2, 0 otherwise;
D2 = 1 if CLASS = 3, 0 otherwise.
Give a 95% confidence interval for:
(a) The difference in expected POST for people in CLASS 3 versus people in
CLASS 1 with the same value of PRE,
(b) The difference in expected POST for people in CLASS 3 versus people in
CLASS 2 with the same value of PRE,
(c) The difference in expected POST for a person in CLASS 3 with PRE = 6 versus a person in CLASS 1 with PRE = 10.
Example 11.3
We are studying the effect of some knowledge of “computer mathematics” on students’ ability to learn trigonometry. The experiment is conducted using students in three classes, which correspond to three treatments (called CLASS) as follows:
CLASS 1: the control class in which students have had no exposure to computer mathematics,
CLASS 2: in which the students were exposed to a course in computer mathematics in the previous semester, and
CLASS 3: in which students have not had a course in computer mathematics, but the first three weeks of the trigonometry class are devoted to an introduction to computer mathematics.
The response variable, called POST, is the students’ scores on a standardized test given at the end of the semester.1 Two variables can be used as a covariate: an aptitude test score (IQ) and a pretest score (PRE) designed to ascertain knowledge of trigonometry prior to the course. The data are shown in Table 11.6. We use the variable PRE as the covariate. The variable IQ is used later in this section.