Sticky Shoe, the discount movie theater, sells popcorn and soda at its concession counter. Cameron, Jessie, and Sean are regular patrons of Sticky Shoe, and the valuations of each for popcorn and soda are as follows:
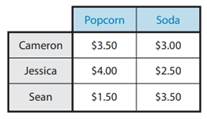
There are 2,997 other residents of Harkinsville who see movies at Sticky Shoe. One-third of them have valuations identical to Cameron, one-third to Jessica, and one-third to Sean. If a customer is indifferent between buying and not, she buys. It costs Sticky Shoe essentially nothing to produce each additional order of popcorn or soda.
(a) If Sticky Shoe sets separate prices for popcorn and soda, what price should it set for each concession to maximize its profit? How much profit does Sticky Shoe make selling concessions separately?
(b) What does each type of customer (Cameron, Jessica, Sean) buy when Sticky Shoe sets separate profit-maximizing prices for popcorn and soda?
(c) Instead of selling the concessions separately, Sticky Shoe decides always to sell the popcorn and soda together in a combo, charging a single price for both. What single combo price would maximize its profit? How much profit does Sticky Shoe make selling only combos?
(d) What does each type of customer buy when Sticky Shoe sets a single profit-maximizing price for a popcorn and soda combo? How does this compare with the answer in part (b)?
(e) Which pricing scheme does each customer type prefer? Why?
(f) If Sticky Shoe sold the concessions both as a combo and separately, which products (popcorn, soda, or the combo) does it want to sell to each customer type? How can Sticky Shoe make sure that each customer type purchases exactly the product that it intends for him or her to purchase?
(g) What prices—for the popcorn, soda, and combo—would Sticky Shoe set to maximize its profit? How much profit does Sticky Shoe make selling the concessions at these three prices?
(h) How do the answers to parts (a), (c), and (g) differ? Explain why.