Please help me with this.
Use element argument to prove the statement. Assume that all sets are subsets of a universal set U, Statement: For all sets A, B, and C, A ∩ (B − C) = (A ∩ B) − (A ∩ C). Please do the proof like the way the example proof does it. Thanks.
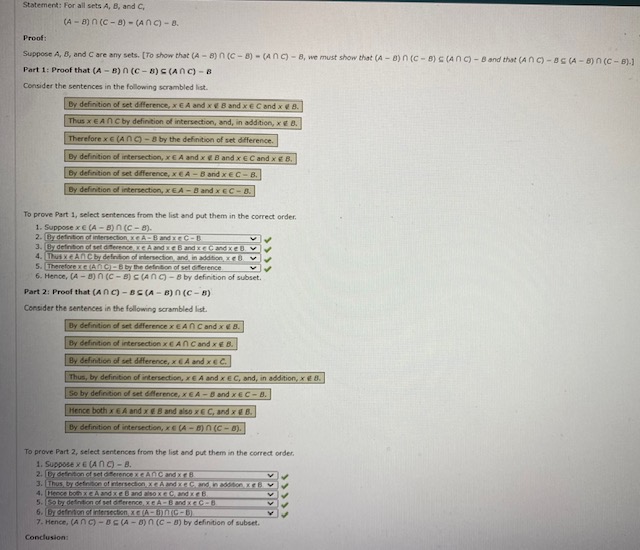
Extracted text: Statement: For all sets A, B, and C, (A - 8)n (C - 8) - (ANC) - 8. Proof: Suppose A, B, and C are any sets. [To show that (A - 8) n (C - 8) - (ANC) - 8, we must show that (A -8)n (C - 8) C (ANC) - B and that (ANC) - 8S ( - 8) n (C - 8).1 Part 1: Proof that (A - B) n (C - 8) S (ANC) - 8 Consider the sentences in the following scrambled list. By definition of set difference, xCA and x EB and xeC and xe 8. Thus x EAN C by definition of intersection, and, in addition, xe 8. Therefore x c (ANg-8 by the definition of set difference. By definition of intersection, xEA and x B and x ECand xe8. By definition of set difference, xeA-B and xEC-B. By definition of intersection, xEA -B and xEC-8. To prove Part 1, select sentences from the list and put them in the correct order. 1. Suppose x€ (A - B) n (C- 8). 2. By defintion of intersection, xe A-Band xeC-B 3. By defintion of set diferencereA and xe B and xeCand KEOV 4. Thus xeANC by definition of intersection and in addition e6 v 5. ThereforexE (ANC-B by the defintion of set diference 6. Hence, (A -8) n (c - 8) C(ANg-8 by definition of subset. Part 2: Proof that (ANC) - BE (A - 8) n (C - B) Consider the sentences in the following scrambled list. By definition of set deference x EAN C and x B. By definition of intersection XEANCand xEB. By definition of set dfference, xEA and xEC. Thus, by definition of intersection, EA and xEC, and, in addition, xe 8. So by definition of set difference, xEA-B and xEC-B. Hence both x EA and xeB and also xe C, and xB. By definition of intersection, xE(A-8)n (C- 8). To prove Part 2, select sentences from the list and put them in the correct order. 1. Suppose xE (ANC)-8. 2. by detinton of set diterencexCANC and xeB 3. Thus, by definition of intersection xe A and xeC and, in addition, eb. 4. (Hence both xCA and xeB andEsoxeCandeE 5. So by defintion of set diferenceXEA-Band xeC-8 6. [By defnton of intersection xE A-BNIC-B) 7. Hence, (ANC) -BE (A - 0) n (C - 8) by definition of subset. Conclusion: >>>>>