
Extracted text: Show that {u,, u2, uz) is an orthogonal basis for R. Then express x as a linear combination of the u's. 3 2 1 4 u1 = - 3 u, = 2 u3 = and x= - 3 - 1 4 1 Which of the following criteria are necessary for a set of vectors to be an orthogonal basis for a subspace W of R"? Select all that apply. O A. The vectors must all have a length of 1. O B. The vectors must span W. O c. The vectors must form an orthogonal set. O D. The distance between any pair of distinct vectors must be constant. Which theorem could help prove one of these criteria from another? O A. If S= {u,, ., u, is an orthogonal set of nonzero vectors in R", then S is linearly independent and hence is a basis for the subspace spanned by S. O B. If S = {u,, ., u, and each u; has length 1, then S is an orthogonal set and hence is a basis for the subspace spanned by S. Oc. If S= {u, ., u,} and the distance between any pair of distinct vectors is constant, then the vectors are evenly spaced and hence form an orthogonal set. O D. If S= {u,, .., u, is a basis in RP, then the members of S span RP and hence form an orthogonal set. Which calculations should be performed next? (Simplify your answers.) O A. u, •u1 = O B. u1 - u2 = O C. u1 •u2 = u2 • U2 = uz • u3 = u, - u3 = u2 - u3 = u, •uz = u2 • u3 = DOC
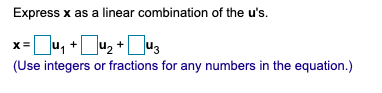
Extracted text: Express x as a linear combination of the u's. x=u, +Ju, +u3 (Use integers or fractions for any numbers in the equation.)