Rewrite the following as a minimization problem (you do not need to solve the problem).
(a) Solve:
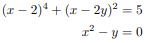
(c) Find the distance between
= 3
−x
+ 5
+ 1 and the point (−1, −2).
(d) The positions of two objects moving in the
-plane are: (
1,
1)=(
+ sin(3),
+ 3 cos(3)), and (
2,
2) = (4 sin
,
2
− 3). How close do they come to bumping into each other?
(e) Two points
p
and
q
are on a surface
=
(). Find a curve on this surface which connects these two points, and which has the smallest length.
(f) Consider a region 0 ≤
≤
, 0 ≤
≤
. Three heaters are going to placed in this region, at points
h
1,
h
2, and
h
3. The resulting temperature
at any point
in the region is
where
()=1/(1+
2). Where should the heaters be placed in the region so the coldest point in the room is as hot as possible?