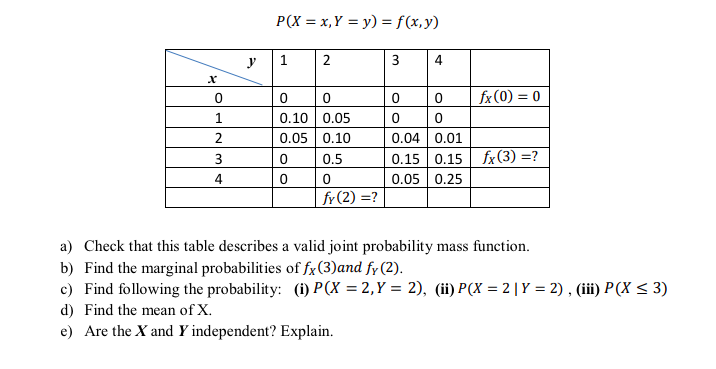
Question 1: Let X and Y denote two discrete random variables taking the values in x and y respectively. The collected data over time is represented in the following stochastic model: ?(? = ?, ? = ?) = ?(?, ?).
a) Check that this table describes a valid joint probability mass function.
b) Find the marginal probabilities of ?? (3)??? ??(2).
c) Find following the probability: (i) ?(? = 2, ? = 2), (ii) ?(? = 2 | ? = 2) , (iii) ?(? ≤ 3)
d) Find the mean of X.
e) Are the X and Y independent? Explain.
Note: Kindly assess the table in the picture attached for more information.
Extracted text: P(X = x,Y = y) = f(x,y) y 1 3 fx(0) = 0 0.10 0.05 0.05 0.10 0.04 0.01 0.15 0.15 fx(3) =? 0.05 0.25 2 3 0.5 4 | fy(2) =? a) Check that this table describes a valid joint probability mass function. b) Find the marginal probabilities of fx(3)and fy (2). c) Find following the probability: (i) P(X = 2,Y = 2), (ii) P(X = 2 | Y = 2) , (ii) P(X < 3)="" d)="" find="" the="" mean="" of="" x.="" e)="" are="" the="" x="" and="" y="" independent?="">