Extracted text: Q2.3 NP-hardness Show that the Control Set problem is NP-hard. Hint: You can use a polynomial-time reduction from Set Cover. You can type your answer directly into the field below. If you do this, please refer to the Gradescope manual for typesetting of maths. Alternatively, you can upload a PDF or an image file with your answer. Enter your answer here E Please select file(s) Select file(s) Save Answer Q2.4 General Assuming that P+NP,which of the following statements are correct? Tick all of them. O The Control Set problem is in NP. O The Control Set problem is a decision problem. O The problem of computing a control set of minimum size for any given input graph is solvable in polynomial time. O The Control Set problem can be solved in time n log n. O A graph G with n vertices has at most n* control sets of size exactly k. Save Answer
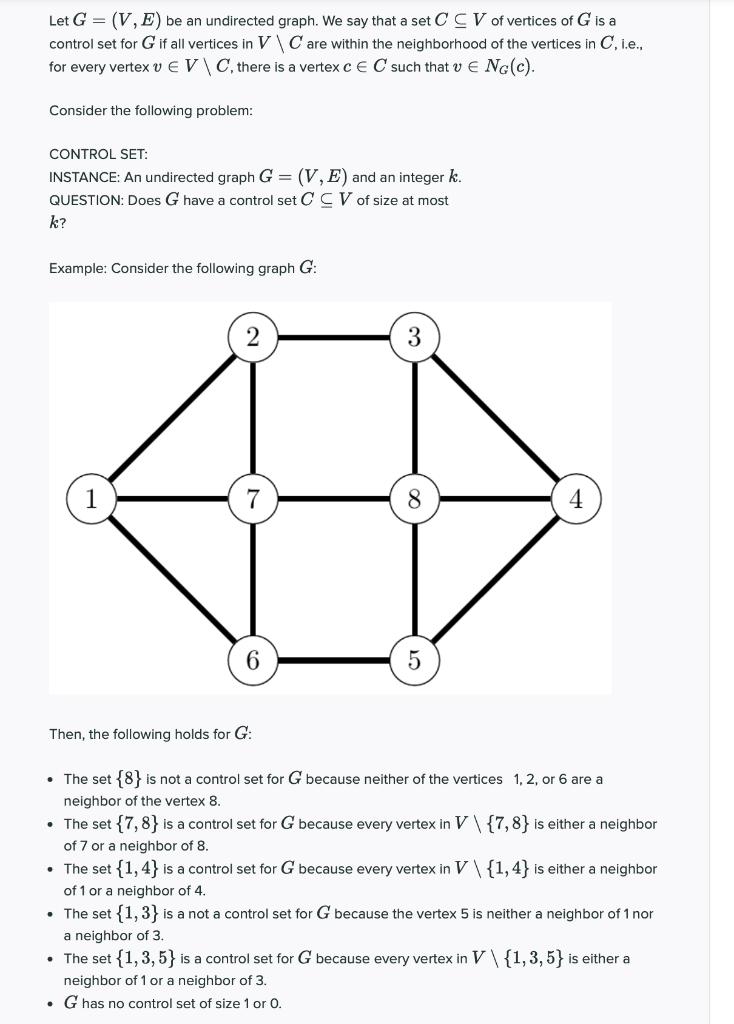
Extracted text: Let G = (V, E) be an undirected graph. We say that a set C C V of vertices of G is a control set for G if all vertices in V\C are within the neighborhood of the vertices in C, i.e., for every vertex v E V \ C, there is a vertex c E C such that v E NG(c). Consider the following problem: CONTROL SET: INSTANCE: An undirected graph G = (V, E) and an integer k. QUESTION: Does G have a control set CCV of size at most k? Example: Consider the following graph G: 1 7 8 4 6 Then, the following holds for G: • The set {8} is not a control set for G because neither of the vertices 1,2, or 6 are a neighbor of the vertex 8. • The set {7,8} is a control set for G because every vertex in V\ {7,8} is either a neighbor of 7 or a neighbor of 8. • The set {1, 4} is a control set for G because every vertex in V\{1,4} is either a neighbor of 1 or a neighbor of 4. • The set {1,3} is a not a control set for G because the vertex 5 is neither a neighbor of 1 nor a neighbor of 3. • The set {1, 3, 5} is a control set for G because every vertex in V\{1,3,5} is either a neighbor of 1 or a neighbor of 3. • G has no control set of size 1 or 0.