Q1.

A manager is ordering 40 inkjet printers for staff working in the company’s main office. Details of the available models are given below. The print quality score has been produced by an independent magazine. The score ranges from 1 = very poor to 5 = excellent.
Use the above information to demonstrate how the manager could apply each of the following strategies to choose the computer and discuss the advantages and disadvantages of using these strategies.
(a) Lexicographic
(b) Semi-lexicographic
(c) Elimination by aspects
(d) Satisficing.
Q2.
After her examinations a student decides that she needs a holiday. A travel agent supplies the following list of last minute holidays that are available. The student works down the list, considering the holidays in the order that they appear until she comes across one that is satisfactory, which she books. Her minimal requirements are:
(i) The holiday must last at least 10 days
(ii) It must cost no more than $1500
(iii) It must not be self-catering
(iv) It must be located in accommodation, which is no more than 5 minutes’ walk from the beach.
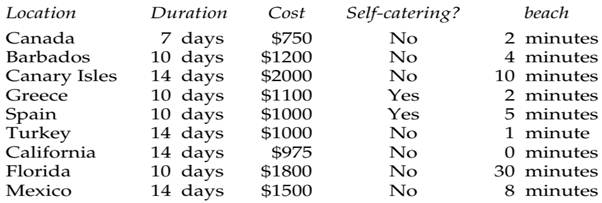
Determine which holiday she will choose from the list below and discuss the limitations of the strategy that she has adopted.
Q3.
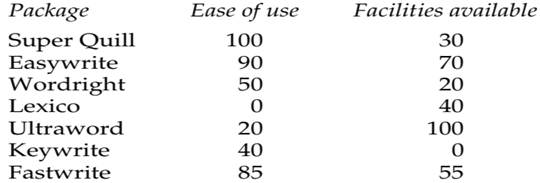
You need a word-processing package for the personal computer in your office. Because your employer will pay for the package you are not concerned about the cost, but you would like a package which is as easy to use as possible and which also has a wide range of functions such as a thesaurus, spell checker and graphics. After discussing the matter with a friend who is something of an expert in this field, you identify seven potential packages and allocate values to them to reflect their ease of use and available facilities. These values are shown below (0 = worst, 100 = best).
(a) Plot each package’s value for ‘ease of use’ and ‘facilities available’ on a graph and hence determine the packages which lie on the efficient frontier.
(b) Suppose that you judge that a switch from a package with the least facilities available to one with the most facilities is only 60% as attractive as a switch from a package which is the least easy to use to one which is the most easy to use. Assuming that mutual preference independence exists between the two attributes, which package should you choose?
(c) After some reflection you realize that the extra facilities available on a package will be of little value to you if they are going to be difficult to use. What does this imply about your method of analysis in (b)?
Q4.
A chemical company is expanding its operations and a disused woollen mill is to be converted into a processing plant. Four companies have submitted designs for the equipment which will be installed in the mill and a choice has to be made between them. The manager of the chemical company has identified three attributes which he considers to be important in the decision: ‘cost’, ‘environmental impact’ and ‘reliability’. He has assessed how well each design performs on each attribute by allocating values on a scale from 0 (the worst design) to 100 (the best). These values are

shown below, together with the costs which will be incurred if a design is chosen.
(a) The manager is having difficulty in allocating weights to the two benefit attributes. Assuming that the two weights sum to 100 and that mutual preference independence exists between the attributes, perform a sensitivity analysis to show how the design offering the highest value for aggregate benefits will vary depending upon the weight which has been allocated to ‘environmental impact’.
(b) Eventually, the manager decides to allocate ‘environmental impact’ a weight of 30 and ‘reliability’ a weight of 70. By plotting the benefits and costs of the designs on a graph, identify the designs which lie on the efficient frontier.
(c) The manager also decides that if he was offered a hypothetical design which had the lowest reliability and the worst environmental impact he would be prepared to pay $120 000 to convert that design to one which had the best impact on the environment but which still had the lowest level of reliability. Which design should the manager choose?
Q5.
A British company has won an important contract to supply components regularly to Poland. Four methods of transport are being considered: (i) air, (ii) sea, (iii) road and ferry and (iv) rail and ferry. The company’s distribution manager has identified four relevant attributes for the decision: Punctuality, Safety of Cargo, Convenience and Costs. She has also allocated weights of 30 to punctuality, 60 to safety of cargo and 10 to convenience.
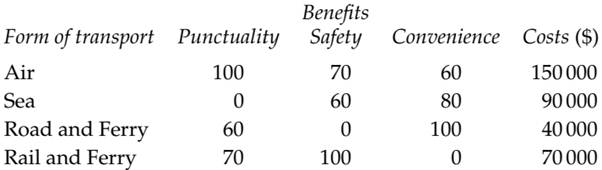
The manager then rated the performance of each form of transport on the different attributes. The values she assigned are shown below together with the estimated annual cost of using each form of transport.
(a) Determine the form of transport which has the highest valued overall benefits, assuming that mutual preference independence exists between the attributes.
(b) For each form of transport, plot the value of overall benefits against costs and hence identify the forms of transport which lie on the efficient frontier.
(c) If the manager would be prepared to pay $70 000 per year to move from the least safe to the most safe form of transport (all else remaining equal), determine which alternative she should select.
Q6.
A local authority has to decide on the location of a new wastedisposal facility and five sites are currently being considered; Inston Common, Jones Wood, Peterton, Red Beach and Treehome Valley. In order to help them to choose between the sites the managers involved in the decision arranged for a decision analyst to attend one of their meetings. He first got the managers to consider the factors which they thought were relevant to the decision and, after some debate, four factors were identified:
(i) The visual impact of the site on the local scenery (for example, a site at Treehome Valley would be visible from a nearby beauty spot).
(ii) The ease with which waste could be transported to the site (for example, Red Beach is only two miles from the main town in the area and is close to a main highway while Inston Common is in a remote spot and its use would lead to a major increase in the volume of transport using the minor roads in the area).
(iii) The risk that the use of the site would lead to contamination of the local environment (e.g. because of leakages of chemicals into watercourses).
(iv) The cost of developing the site.

The decision analyst then asked the managers to assign scores to the sites to show how well they performed on each of the first three attributes. The scores they eventually agreed are shown below, together with the estimated cost of developing each site. Note that 0 represents the worst and 100 the best score on an attribute. In the case of risk, therefore, a score of 100 means that a site is the least risky.
The decision analyst then asked the managers to imagine a site which had the worst visual impact, the most difficult transport requirements and the highest level of risk. He then asked them if they had a chance of switching from this site to one which had just one of the benefits at its best value, which would they choose?
The managers agreed that they would move to a site offering the least risk of contamination. A move to a site with the best visual impact was considered to be 80% as preferable as this, while a move to one with the most convenient transport facilities was 70% as preferable.
(a) Can we conclude from the values which were assigned to the different sites for visual impact that, in terms of visual impact, the Inston Common site is five times preferable to Red Beach? If not, what can we infer from the figures?
(b) An alternative way of allocating weights to the three benefit attributes would have involved asking the managers to allocate a score reflecting the importance of each attribute. For example, they might have judged that risk was five times more important and visual impact three times more important than ease of transport, so that weights of 5, 3 and 1 would have been attached to the attributes. What are the dangers of this approach?
(c) Assuming that mutual preference independence exists between the attributes, determine the value of aggregate benefits for each site.
(d) Plot the aggregate benefits and costs of each site on a graph and hence identify the sites which lie on the efficient frontier.
(e) Although a weight of 80 was finally agreed for visual impact, this was only after much debate and some managers still felt that a weight of 65 should have been used while others thought that 95 would have been more appropriate. Perform a sensitivity analysis on the weight assigned to visual impact to examine its effect on the aggregate benefits of the sites and interpret your rresults.
Q7.
As an experiment, a charity decides to use the SimpleMulti-attributeRating Technique (SMART) to determine a short list from the seven applicants who have applied for the post of Regional Officer for the Western region. The main criteria which will be used to compare candidates are: the salary they would expect (SALARY) (they have stated this on the application form), their experience of charity work (CHARITY EXP), their managerial experience (MANAGEMENT EXP), their educational qualifications (EDUCATION), their apparent commitment to the charity’s work (COMMITMENT) (as gleaned from the application form) and the quality of the ideas they put forward on the form (IDEAS).
(a) When a value tree was used to identify the above attributes there was some doubt about whether the attributes IDEAS and COMMITMENT met Keeney and Raiffa’s criterion of decomposability. Explain what this means and why the concerns might be justified.
(b) The personnel manager ranked all the criteria, except salary, in order of importance and then assigned weights as follows:
COMMITMENT 100
MANAGEMENT EXP 70
IDEAS 65
CHARITY EXP 55
EDUCATION 10
(Note that, on the basis of the application form, all of the candidates appeared to be equally committed to the charity.)
Discuss whether the method the personnel manager used to assess these weights is appropriate.
(c) Candidate A’s scores for the non-monetary attributes are given
below:
COMMITMENT 100
MANAGEMENT EXP 10
IIDEAS 65
CHARITY EXP 0
EDUCATION 10
Using the weights given in part (b) show how the personnel manager obtained a score of 50 (subject to rounding) for this candidate.
(d) The aggregate scores for all the candidates are given below, together with their expected salaries. Assuming that the personnel manager’s model is appropriate, determine the candidates who appear on the efficient frontier and explain the significance of this.
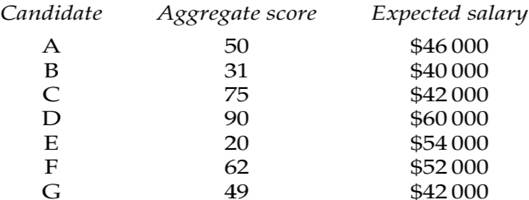
(e) The candidate with the least management experience has only been working in management for two years, while the most experienced candidate has 10 years’ experience. If the personnel manager reckons that the charity would be prepared to pay $8000 for the eight years’ extra management experience, all else remaining equal, determine which candidate she should recommend for the appointment prior to the interview. State any assumptions you have made.
Q8.
The owner of a small business is unhappy with the service she has been receiving from her bank and has decided to move her account to a rival bank. Her decision on which bank to choose will be based not only on the estimated annual bank charges which each bank will levy, but also on the following ‘benefit attributes’:
(a) the proximity of the local branch,
(b) whether the local branch has a small business adviser,
(c) the maximum automatic loan allowed,
(d) whether a telephone banking facility is offered.
The alternative banks are listed below, together with their estimated annual costs and the scores the business owner has allocated for each of the ‘benefit attributes’.

The business owner is then asked to imagine that she has her account with a hypothetical bank which had the lowest scores on all of the ‘benefit attributes’. She is then asked to imagine that each attribute could be switched to its best possible value and asked to rank the attractiveness of these possible switches. Her ranks are given as:
Rank Switch
1 Lowest maximum loan facility to highest
2 No telephone banking facility to existence of this facility
3 Non-availability of small business adviser to availability
4 Least close branch to closest branch
(a) SMARTER has been used to obtain scores to represent the aggregate benefits of the banks and these are given below: Show how the score of 35.4 for the Central bank was determined.
Bank Aggregate score
Central 35.4
Northern 62.5
Direct 83.5
Royal 29.0
Marks 30.6
(b) Explain why it was appropriate to consider swings (or switches) from the worst to best positions on each attribute when determining the weights of the attributes.
(c) By taking into account the estimated annual charges of the banks, determine which banks lie on the efficient frontier. Explain the significance of the efficient frontier.
(d) SMARTER is based on the ‘principle of heroic approximation’. Explain how this principle applies to your analysis of the businesswoman’s problem and discuss whether it is likely to be appropriate.
Q9.
A food company has to buy a new packaging machine and the list of possible machines has been reduced to five: the Allstar, Belle, Cardigan, DRT and Ellton. The decision on which machine to buy will be based on five attributes: (i) costs, (ii) the quality of the after-sales service provided by the supplier (AFTER SALES), (iii) the extent to which the supplier will customize the machine to meet the specific needs of the food manufacturer (CUSTOMIZATION), (iv) the earliest date when the machine can be delivered (DELIVERY) and (v) the machine’s reputation for reliability (RELIABILITY).
The costs of the machines are given below, together with values which the company’s production manager has assigned to them for the non-monetary attributes (0 = worst, 100 = best).

(a) The values for the non-monetary attributes have been measured on an interval scale. Use the values assigned to AFTER SALES to explain what this means.
(b) The manager was asked to imagine a hypothetical machine which has the worst characteristics of all the machines on the non-monetary attributes. She was then offered the chance to change one of this machine’s attributes to that of the best machine on this attribute. After some thought, she decided that she would most prefer to change RELIABILITY to the best level. She considered similar changes in AFTER SALES, CUSTOMIZATION and DELIVERY to be, respectively, 50%, 80% and 10% as desirable as the change in RELIABILITY. These judgments were used to derive the following aggregate scores for the non-monetary benefits of the machines.
MachineAllstar Belle Cardigan DRT Ellton
Score 26.25 83.33 66.25 31.67 87.50
(i) Show how the score for the Allstar machine was obtained.
(ii) By plotting the costs of the machines against their scores, identify the machines that lie on the efficient frontier.
(c) Explain the role that sensitivity analysis could play in helping the manager to reach a decision.
Q10.
The organizers of an international conference have to choose a hotel that will be the conference venue. The organizers started with an initial list of 40 possible hotels, but this has now been reduced to a short list of five: the Alton, the Buttermere, the Castle, the Dorset and the Elm. A value tree was used to identify the attributes relating to the decision. These are (i) the cost of using the hotel, (ii) ease of transport to the hotel, (iii) quality of the conference facilities, (iv) comfort of the bedrooms and (v) quality of other facilities.
(a) The value tree was found to meet Keeney and Raiffa’s five criteria of completeness, operationality, decomposability, absence of redundancy and minimum size. Explain what these criteria will mean in the context of the problem.
(b) The costs of using the hotels for the conference are given below, together with scores that the organizers assigned to them for the non-monetary attributes (0 = worst performance on the attribute, 100 = the best).
The organizers were then asked to consider a hypothetical hotel which had the lowest scores on all of the non-monetary attributes. They were then asked to imagine that each of this hotel’s attributes could be switched to its best possible value (all else remaining equal) and asked to rank, and then weight, the attractiveness of these possible switches. The results are given below.
Attribute Weight
Transport 80
Conference facilities 100
Comfort 50
Other facilities 20
One of the organizers, who was not present during the decision analysis session, expresses concern that ease of transport to the hotel was acknowledged as being the most important attribute, yet it has not been given the largest weight. Explain why the weights might still be valid.
(c) SMART has been used to obtain aggregate scores for the nonmonetary attributes and the results are given below. Show how the score for the Alton hotel was obtained.
(d) What would Alton’s score have been if rank-sum weights had been used, instead of the weights given above?
(e) Which hotels lie on the efficient frontier when costs are brought into consideration?
(f) The organizers would be willing to pay $6000 if a hotel’s conference facilities could be upgraded from those equivalent to the worst to those equivalent to the best, all else remaining equal. Determine which hotel they should choose, stating any assumptions you have made.
Q11.
A national television company is hoping to set up an MA course in Media Management for its managerial staff, in collaboration with a university. Five universities have submitted bids for the course and the television company has to make a decision between them. The company has identified five attributes that are relevant to its decision problem: (i) the quality of the university’s staff, (ii) the proposed course structure, (iii) the teaching facilities available at the university, (iv) the residential facilities available on the university campus and (v) the cost of the course. For each of the non-monetary attributes the company has allocated scores to the universities to assess their performance on that attribute (0 = worst performance on that attribute, 100 = best). The results are given below.
The company then considered the case of a hypothetical university that had the worst performance on all the non-monetary attributes. It then considered which improvement it would most like to make to this university’s proposal. It was agreed that improving the course structure to that equivalent to the best course structure would be the most desirable. Improvements from the worst to best performance in staff, teaching facilities and residential facilities were respectively considered to be 30%, 60% and 40% as important as the improvement in course structure.
(a) When the Simple Multi-attribute Rating Technique (SMART) was applied to the scores and weights the following aggregate scores were obtained for the non-monetary attributes.
University Aggregate score
Barchester 66.96
Cramwich 65.65
Denford 53.04
Enton 26.09
Flowton 34.35
Show how the score for Barchester university was obtained.
(b) Identify the universities which lie in the efficient frontier.
(c) The company would be prepared to pay $30 000 for an improvement in a university’s teaching facilities from that equivalent to the worst university to that equivalent to the best (all else remaining equal). Identify the university it should choose (assuming that the original weights apply).
(d) The intuitive choice of the television company’s managers differs from that recommended by your SMART model. Briefly discuss why this discrepancy may have arisen and how it might be resolved.
Q12.
Determine the probability of each of the following events occurring. State the approach to probability which you used and any assumptions which you needed to make.
(a) A person selected from the payroll of a company is a clerical worker given that there are 350 people on the payroll of whom 120 are clerical workers.
(b) A light bulb selected from a production line is defective if, out of 400 bulbs already tested, eight were defective.
(c) A new-born baby is male.
(d) This month’s sales forecast for a product has an error of more than 10% if the forecast had an error of over 10% in 21 out of the last 60 months.
(e) A permanently manned space station is established on Mars by the year 2050.
Q13.
The following table shows an estimated probability distribution for the sales of a new product in its first week:
Number of units sold 0 1 2 3 4 5
Probability 0.05 0.15 0.20 0.35 0.15 0.10
What is the probability that in the first week:
(a) Four or five units will be sold;
(b) At least 3 units will be sold;
(c) At least 1 unit will be sold?
Q14.
The managers of a food company are interested in determining the effect on their sales of a competitor’s television advertisements. An analysis of sales records for the last 120 weeks gives the following results:
Assuming that these past data are a reliable guide to the future, determine the probability that next week:
(a) The competitor will advertise;
(b) Sales will not be high;
(c) Medium or high sales will be achieved;
(d) Either the competitor will advertise or only low sales will be achieved;
(e) Either the competitor will not advertise or high sales will be achieved.
Q15.
(a) With reference to the table in question 3, determine the following probabilities:
(i) p(next week’s sales will be high)
(ii) p(next week’s sales will be high|the competitor advertises)
(iii) p(next week’s sales will be high|the competitor does not advertise)
(iv) p(next week’s sales will be low)
(v) p(next week’s sales will be low|the competitor advertises)
(b) Do the events ‘competitor advertises’ and ‘high sales’ appear to be independent?
Q16.
Given below are the results of a survey of 100 cars:
Condition of brakes
Condition of tires Faulty Not faulty Total
Faulty 25 5 30
Not faulty 15 55 70
Total 40 60 100
(a) Assuming that the survey is representative of all the cars on the road, what is the probability that a car selected at random will have:
(i) Faulty brakes;
(ii) Faulty tires;
(iii) Either faulty brakes or faulty tires;
(iv) Faulty brakes given that it has faulty tires;
(v) Faulty tires given that it has faulty brakes?
(b) What conclusion would you draw about the relationship between the events ‘faulty tires’ and ‘faulty brakes’?
Q17.
A speculator purchases three stocks on the London Stock Exchange. He estimates that the probabilities that each of these stocks will have risen in value by the end of the week are, respectively, 0.6, 0.8 and 0.4.
(a) Assuming that the price changes in the three stocks are independent, determine the probability that all three stocks will have risen in value by the end of the week.
(b) Do you think that it is reasonable to assume that movements in the prices of individual stocks are independent?
Q18.
The managers of a company are considering the launch of a new product and they are currently awaiting the results of a market research study. It is thought that there is a 0.6 probability that the market research will indicate that sales of the product in its first three years will be high. If this indication is received then the probability that sales will be high is thought to be 0.8. What is the probability that the market research will indicate high sales and sales will turn out to be high?
Q19.
An engineer at a chemical plant wishes to assess the probability of a major catastrophe occurring at the plant during the overhaul of a processor as a result of a malfunction in the equipment being used in the overhaul. He estimates that the probability of a malfunction occurring is 0.1. If this happens there is only a 0.001 probability that a safety device will fail to switch off the equipment. If the safety device fails the probability of a major catastrophe is estimated to be 0.8. What is the probability that a major catastrophe will occur at the plant during the overhaul as a result of the equipment malfunctioning?
Q20.
The probability of the Dow-Jones index rising on the first day of trading next week is thought to be 0.6. If it does rise then the probability that the value of shares in a publishing company will rise is 0.8. If the index does not rise then the publishing company’s shares will only have a 0.3 probability of rising. What is the probability that the publishing company’s shares will rise in value on the first day of trading next week?
Q21.
A company has two warehouses to sell, one in the town of Kingstones and another in the nearby suburb of Eadleton. Because there have been some indications that property prices are likely to rise over the next six months some of the managers of the company are urging that the sale should be delayed. It is thought that the probability of the Kingstones warehouse rising in value by at least 10% is 0.6. If it does rise in value by this amount then there is a 0.9 probability that the Eadleton property will also rise in value by at least 10%. However, if the Kingstones property rises in value by less than 10% there is only a 0.3 probability that the Eadleton warehouse will increase its value by at least 10%. What is the probability that (a) both warehouses; (b) only one warehouse will increase in value by at least 10% over the six-month period?
Q22.
A car owners’ club which offers a rescue service for stranded motorists has to make a decision on the number of breakdown patrols to deploy between midnight and 8 a.m. on weekdays during the summer. The number of requests for assistance received by a local office during these hours follows the probability distribution shown below.
No. of requests received 0 1 2 3 4 5
Probability 0.01 0.12 0.25 0.42 0.12 0.08
(a) Calculate the expected number of requests received and interpret your results.
(b) Is this a discrete or a continuous probability distribution?
Q23.
You are thinking of selling your house and you reckon that there is a 0.1 probability that you will sell it for $120 000, a 0.5 probability that you will receive $100 000 for it and a 0.4 probability that you will only receive $80 000. What is the expected selling price of the property? Interpret you result.
Q24.
A toll bridge over the River Jay is operated by a private company who are thinking of installing automatic machines to collect the tolls. These machines, however, are not perfectly reliable and it is thought that the number of breakdowns occurring per day would follow the probability distribution shown below:
Number of breakdowns per day
0 1
Probability 0.4 0.6
When a breakdown occurred, revenue from tolls would be lost until the equipment was repaired. Given below are approximate probability distributions for the equipment repair time and the average revenue lost per hour.
[Equipment repair time] [Probability] [Average revenue lost per hour] [Probability]
1 hour 0.7 $40 0.6
2 hours 0.3 $50 0.3
$60 0.1
(a) Determine the probability distribution of revenue which would be lost per day as a result of machine breakdowns (it can be assumed that the above probability distributions are independent).
(b) Calculate the expected loss of revenue per day and interpret your result.
Q25.
An entertainment company is organizing a pop concert in London. The company has to decide how much it should spend on publicizing the event and three options have been identified:
Option 1: Advertise only in the music press;
Option 2: As option 1 but also advertise in the national press;
Option 3: As options 1 and 2 but also advertise on commercial radio.
For simplicity, the demand for tickets is categorized as low, medium or high. The payoff table below shows how the profit which the company will earn for each option depends on the level of demand.
Demand
Option Low Medium Medium High Profits ($000s)
1 −20 −20 100
2 −60 −20 60
3 −100 −60 20
It is estimated that if option 1 is adopted the probabilities of low, medium and high demand are 0.4, 0.5 and 0.1, respectively. For option 2 the respective probabilities are 0.1, 0.3 and 0.6 while for option 3 they are 0.05, 0.15 and 0.8. Determine the option which will lead to the highest expected profit. Would you have any reservations about recommending this option to the company?
Q26.
A speculator is considering the purchase of a commodity which he reckons has a 60% chance of increasing in value over the next month. If he purchases the commodity and it does increase in value the speculator will make a profit of about $200 000, otherwise he will lose $60 000.
(a) Assuming that the expected monetary value criterion is applicable, determine whether the speculator should purchase the commodity.
(b) Perform a sensitivity analysis on the speculator’s estimate of the probability of a price increase and interpret your result.
(c) What reservations would you have about applying the expected monetary value criterion in this context?
Q27.
A team of scientists is due to spend six months in Antarctica carrying out research. One major piece of equipment they will be taking is subject to breakdowns caused by the sudden failure of a particular component. Because a failed component cannot be repaired the team intend to carry a stock of spare units of the component, but it will cost them roughly $3000 for each spare unit they take with them. However, if the equipment breaks down and a spare is not available a new unit will have to be specially flown in and the team will incur a total cost of $4000 for each unit that is delivered in this way. An engineer who will be traveling with the team has estimated that the number of spares that will be required during the six months follows the probability distribution shown below:
No. of spares required 0 1 2 3
Probability 0.2 0.3 0.4 0.1
Determine the number of spares that the team should carry if their objective is to minimize expected costs.
Q28. Y
ou are a contestant on a television game show and you have won $5000 so far. You are now offered a choice: either you can keep the money and leave or you can continue into the next round, where you have a 70% chance of increasing your winnings to $10 000 and a 30% chance of losing the $5000 and finishing the game with nothing.
(a) Which option would you choose?
(b) How does your choice compare with that which would be prescribed by the expected monetary value criterion?
Q29.
A building contractor is submitting an estimate to a potential customer for carrying out some construction work at the customer’s premises. The builder reckons that if he offers to carry out the work for $150 000 there is a 0.2 probability that the customer will agree to the price, a 0.5 probability that a price of $120 000 would eventually be agreed and a 0.3 probability that the customer will simply refuse the offer and give the work to another builder. If the builder offers to carry out the work for $100 000 he reckons that there is a 0.3 probability that the customer will accept this price, a 0.6 probability that the customer will bargain so that a price of $80 000 will eventually be agreed and a 0.1 probability that the customer will refuse the offer and take the work elsewhere.
(a) Determine which price the builder should quote in order to maximize the expected payment he receives from the customer.
(b) Suppose that, after some questioning, the builder is able to make the following statements:
‘I am indifferent between receiving $120 000 for certain or entering a lottery that will give me a 0.9 probability of $150 000 and a 0.1 probability of winning $0.’
‘I am indifferent between receiving $100 000 for certain or entering a lottery that will give me a 0.85 probability of winning $150 000 and a 0.15 probability of winning $0.’
‘I am indifferent between receiving $80 000 for certain or entering a lottery that will give me a 0.75 probability of winning $150 000 and a 0.25 probability of winning $0.’
(i) Sketch the builder’s utility function and comment on what it shows.
(ii) In the light of the above statements which price should the builder now quote to the customer and why?
Q30.
(a) Use the following questions to assess your own utility function for money values between $0 and $5000. You should assume that all sums of money referred to will be received immediately.
(i) You are offered either a sum of money for certain or a lottery ticket that will give you a 50% chance of winning $5000 and a 50% chance of winning $0. Write down below the certain sum of money which would make you indifferent between whether you received it or the lottery ticket.
$ ......... (we will now refer to this sum of money as X)
The utility of X is 0.5.
(ii) You are now offered a lottery ticket which offers you a 50% chance of $ ......... (enter X here) and a 50% chance of $0. Alternatively, you will receive a sum of money for certain. Write down below the certain sum of money which would make you indifferent between whether you received it or the lottery ticket.
$ .........
The utility of this sum of money is 0.25.
(iii) Finally, you are offered a sum of money for certain or a lottery ticket which will give you a 50% chance of $5000 and a 50% chance of $......... (enter X here). Write down below the certain sum of money which would make you indifferent between whether you received it or the lottery ticket.
$.........
The utility of this sum of money is 0.75.
(b) Plot your utility function and discuss what it reveals.
(c) Discuss the strengths and limitations of the assessment procedure which was used in (a).