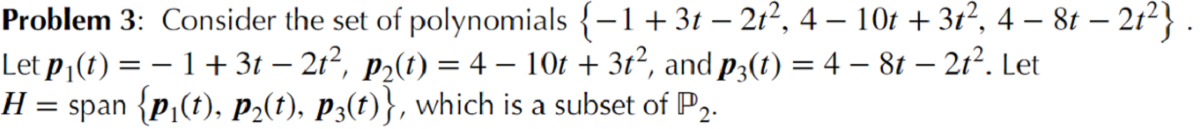
Extracted text: Problem 3: Consider the set of polynomials {-1+3t – 21², 4 – 10t + 3t², 4 – 8t – 21²} . Let p¡(t) = – 1 + 3t – 21², p2(t) = 4 – 10t + 3ť², and p3(t) = 4 – 8t – 21². Let H = span {p,(t), P2(t), P3(t)}, which is a subset of P,.

Extracted text: Use the standard basis for P, B = {1, t, t2}, and the coordinate mapping to show that 10 – 12t – 25t² is in H, and use this to write 10 – 12t – 25t? as a linear combination of P¡(t), p2(t), and, p3(t). Please show all work! Is the polynomial 3 – 3t in H? If you answer yes, write 3 – 3t as a linear combination of P,(t), P2(t), and, p3(t). If no, make sure your work is clear as to why not. - Does the set of polynomials {-1+ 3t – 2t?, 4 10t + 3t2, 4 – 8t – 2t2} span P,? Why -