Options are :
equals the real number 0
is the position vector of D
is a real number greater than 0
is a vector equation for the plane M
is the position vector of the midpoint of the line segment DB
is the position vector of a point that lies on the plane M but does not lie on any of the line segments AB,AC or BC
is the position vector of a point not lying on the plane M
is a vector equation for a plane that passes through A but not through B
is the position vector of the midpoint of the line segment AC
is the position vector of A
is a real number less than 0
is a meaningless expression
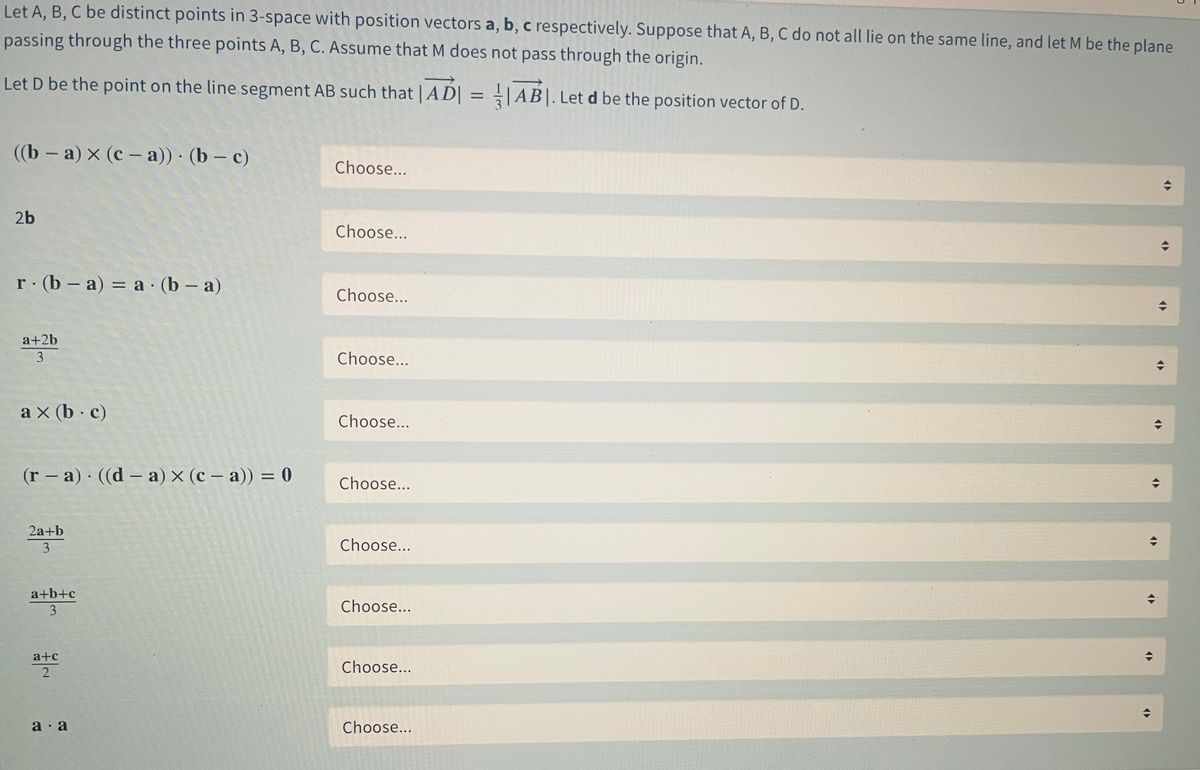
Extracted text: Let A, B, C be distinct points in 3-space with position vectors a, b, c respectively. Suppose that A, B, C do not all lie on the same line, and let M be the plane passing through the three points A, B, C. Assume that M does not pass through the origin. Let D be the point on the line segment AB such that | AD| = |AB|. Let d be the position vector of D. (b — а) x (с- а)) (b - с) Choose... 2b Choose... r (b – a) = a · (b – a) %3D Choose... a+2b 3 Choose... a x (b c) Choose... (r – a) ((d – a) × (c – a)) = 0 %3D | | Choose... 2а+b 3 Choose... a+b+c 3 Choose... a+c Choose... a · a Choose... 2.