(Optional, for mathematically trained students) In the three-type evolutionary game of Section 5 and Figure 12.11, let q XXXXXXXXXXq1 2 q2 denote the proportion of the orange-throated aggressor types....

(Optional, for mathematically trained students) In the three-type evolutionary game of Section 5 and Figure 12.11, let q3 5 1 2 q1 2 q2 denote the proportion of the orange-throated aggressor types. Then the dynamics of the population proportions of each type of lizard can be stated as

And

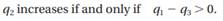
We did not state this explicitly in the chapter, but a similar rule for q₃
is

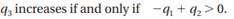
(a) Consider the dynamics more explicitly. Let the speed of change in a variable x in time t be denoted by the derivative dxdt. Then suppose

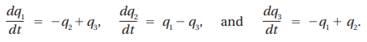
Verify that these derivatives conform to the preceding statements regarding the population dynamics.

(b) Define
  Using the chain rule of differentiation, show that dXdt 5 0, that is, show that X remains constant over time.

(c) From the definitions of the entities, we know that q₁
+ q₂
+ q₃
= 1. Combining this fact with the result from part (b) show that over time, in three-dimensional space, the point (q₁, q₂, q₃) moves along a circle.

(d) What does the answer to part (c) indicate regarding the stability of the evolutionary dynamics in the colored-throated lizard population?