Open Word and answer the following questions. Save the document and print it when you are done. 1. A Cobb-Douglas production function with increasing returns to scale yields a total cost function that...

Open Word and answer the following questions. Save the document and print it when you are done.

1. A Cobb-Douglas production function with increasing returns to scale yields a total cost function that increases at a decreasing rate. Use Word’s Drawing Tools to draw the underlying isoquant map for such a production function. Hint: The spacing between the isoquants is crucial.

A commonly used specification for production functions in empirical work is the translog functional form. There are several versions. When applied to the cost function, you get a result like this:

Notice that the function is a modification of the log version of a CobbDouglas function. In addition to the individual log terms there are combinations of the three variables, called interaction terms.

Click the Exercise Questions button at the bottom of the Q&A sheet in the CostCurves.xls workbook to reveal a sheet with translog cost function parameters. Use this sheet to answer the following questions.

2. Enter a formula in cell B18 for the TC of producing 100 units of output, given the alpha coefficient and input price values in cells B5:B13. Fill your formula down and then create a chart of the total cost function (with appropriate axes labels and a title). Copy and paste your chart in your Word document. Hint: TC = e^{ln TC}
and Exp(number) in Excel returns e raised to the to the power of number.

3. Compute MC via the change in output from 100 to 110 in cell C19. Report your result.

4. Compute MC via the derivative at Q = 100 in cell D18. Report your result. Hint:

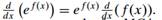
5. Compare your results for MC in questions 3 and 4 – are your answers the same or different? Explain.