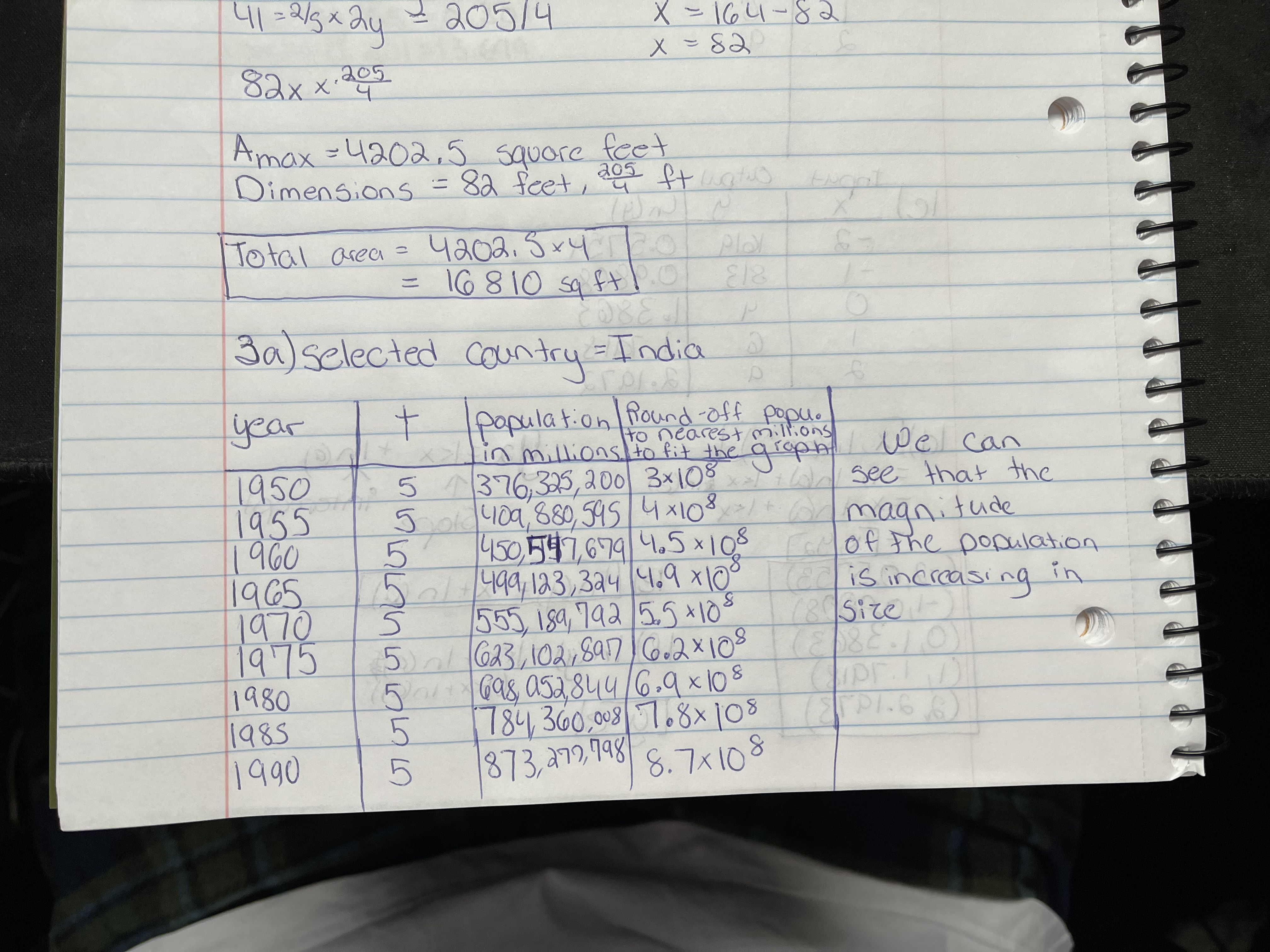
ONLY f, fi, fii3. Choose a country and research population data in order to fill out the table below
INIDAa. Copy the population numbers counted each five years, as shown in the data base, for
the years from 1950 to 2000. Add a column, t, measuring years since 1945.
Year |
t |
population |
1950 |
5 |
376,325,200 |
1955 |
5 |
409,880,595 |
1960 |
5 |
450,547,679 |
1965 |
5 |
499,123,324 |
1970 |
5 |
555,189,792 |
1975 |
5 |
623,102,897 |
1980 |
5 |
698,952,844 |
1985 |
5 |
784,360,008 |
1990 |
5 |
873,277,798 |
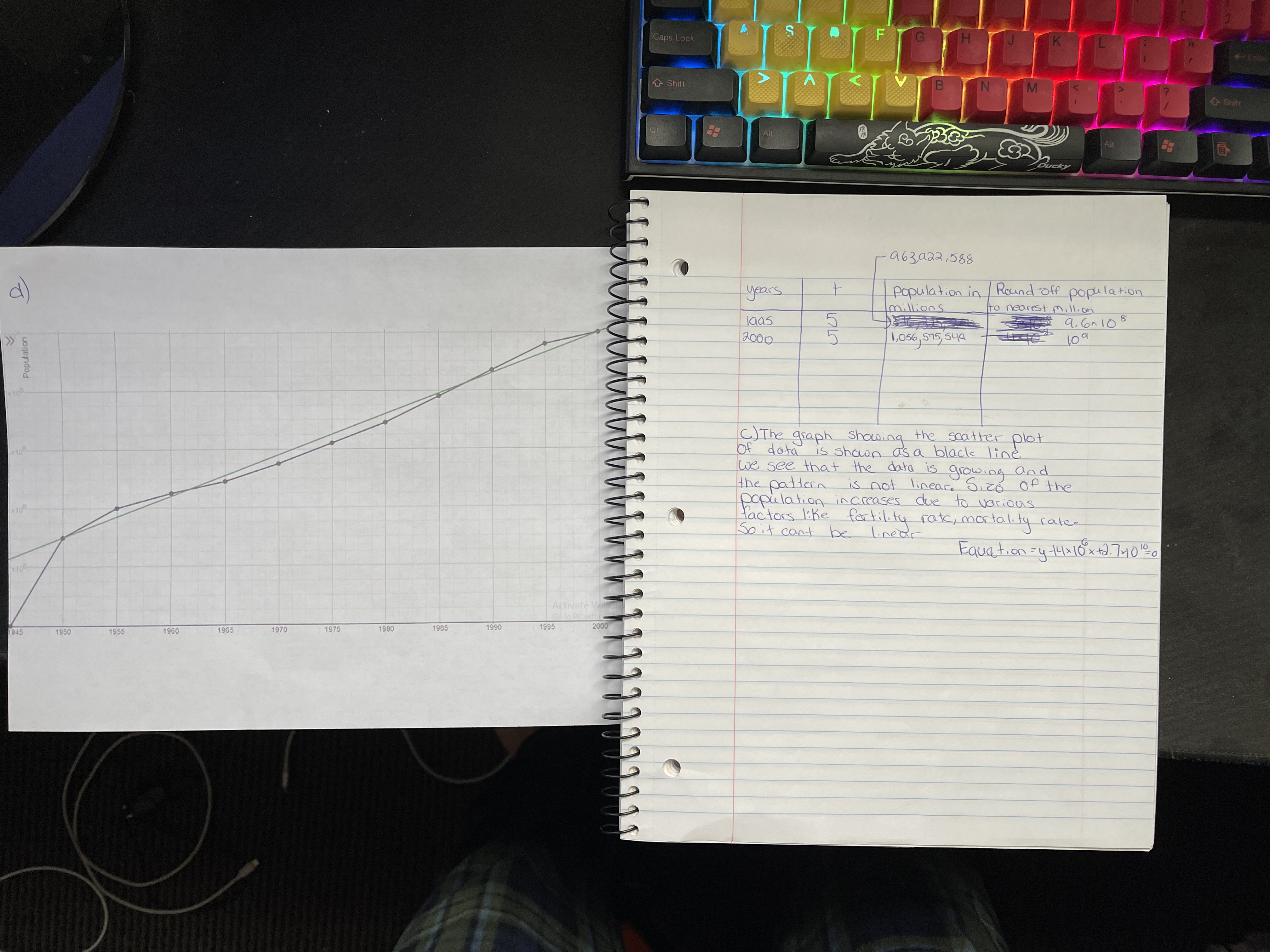
1995 |
5 |
963,922,588 |
2000 |
5 |
1,056,575,549 |
b. What is the country you selected? In what part of the world is it? What is the magnitude
of its population numbers? (100,000’s, millions, hundred millions, billions?) Is it growing or
shrinking in population size?
c. Enter years since 1945 and your population numbers into your graphing calculator.
Create a scatterplot of the data. Is the data growing or shrinking? Does it appear to be a
linear pattern or non-linear? Explain your conclusions.
d. Use your calculator to fit a linear model to the population size.
i. Write the equation of the linear regression and superimpose its graph on your scatterplot.
ii. Use TI-Connect to copy the scatterplot onto your write-up, or just draw a sketch of it.
iii. How well does the linear model fit your data?
iv. What is the vertical intercept of the regression model? What does it mean in the context
of the population?
v. What is the slope of the regression model? What does it mean in the context of the
population?
vi. Use the model to predict the population size in the year you were born. Also, use the
model to predict the population size in the year 2007.
e. Next fit an exponential model to your population data.
i. Write the equation of the exponential regression and superimpose its graph on your
scatterplot.
ii. How well does the exponential model fit your data? By looking at the graphs, does it
appear that the exponential model fits better than the linear model?
f. Next fit a power function to your population data.
i. Write the equation of the power regression and superimpose its graph on your
scatterplot.
ii. How well does the power model fit your data? By looking at the graphs, which of the
three models seems to fit the best?
g. Find the linear correlation coefficient for each model and compare them to determine
which model fits the data best.
Extracted text: 205/4 X164-82 82xx 205 Amax =4202,5 squore feet = 82 feet, ftao 205 y202.3xyO =16810 sq ftlo Total area = Play ニ 813 Ja)selected ountry=India population|found-off popu. nearest millions in millions to fit the qroph graph ilo/ year lWecan see that the 1950 1955 1960 1965 1970 1975 1980 1985 1990 5 376,325,200 3x108 5 409,880,545 4x103/O magnitude 450,547,679 4.5x108 5011499,123,3a4 4.9 x10° reMof the population (80 is increasing in (89Size-) 555, 189, 792 5.5*10$ 5) 623,102,8a7 Coo2x108 5mdGas a5a844/6.9x108 784360,008 7.8×108 8.7x108 Pl.6.6) 5. 873,272, 798
Extracted text: LL Caps Lock G. H. K Ene A Shift B N Shift Alt Alt Bucky a63,922,588 d) population in/ Round off popilation millions yoars to nearest Million jaas 5. 9,6x10 109 2000 L,os6,575 5ya ,056. sto C)The graph showing the scatter plot of data we see that the data is growing and the pattern population increases due to varioas factors :Ke fortil.ty rate, mortality rater So it cant be is shown as a blackk linė is not lineace Sizó of the 10 linedr Equat.on=yt4x10x tQ. 7MO o Activate Win Go to PC dettir 1995 1965 1970 1975 1980 1985 1990 2000 1945 1950 1955 1960 Population