On a Sunday afternoon a professor thinks at home about the question, if similarity solutions exist for the following problem: A sphere, which is very large and can be considered to be half-infinite in...

On a Sunday afternoon a professor thinks at home about the question, if similarity solutions exist for the following problem: A sphere, which is very large and can be considered to be half-infinite in size, is hollow (r = r₁). At the beginning the sphere has a constant temperature T = T₀
everywhere. Then, suddenly the temperature at r = r₁
is changed to T = T₁
for t > 0. For very large radii, the temperature of the sphere stays always at T0. All properties of the sphere (ρ, c, k) are constant. The temperature distribution in the sphere can be calculated by solving the heat conduction equation. This equation is given in spherical coordinates by

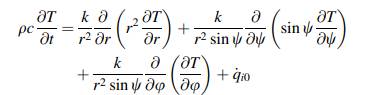
In this equation r is the radial coordinate, φ, ψ denote the tangential and azimuthal coordinates. The term q_i0 denotes sources or sinks in the domain.

(a) Simplify the heat conduction equation under the assumption of onedimensional transient heat conduction.

(b) Introduce the dimensionless temperature H = ( ) T  T0 =( ) T1  T0 into the energy equation and formulate the boundary conditions for r = r1 and for r ! 1.

(c) Please now support the professor in searching for similarity solutions for this differential equation. For this, introduce

s = t

g = rg(s)

into the equation and derive an equation for H = f(g) .

(d) Which condition has to be satisfied for g(τ), so that self-similar solutions can be obtained for this problem? Derive now the ordinary differential equation for H(g)g . Insert in this equation the substitution z = g₂H₀
and derive a solution for the problem.