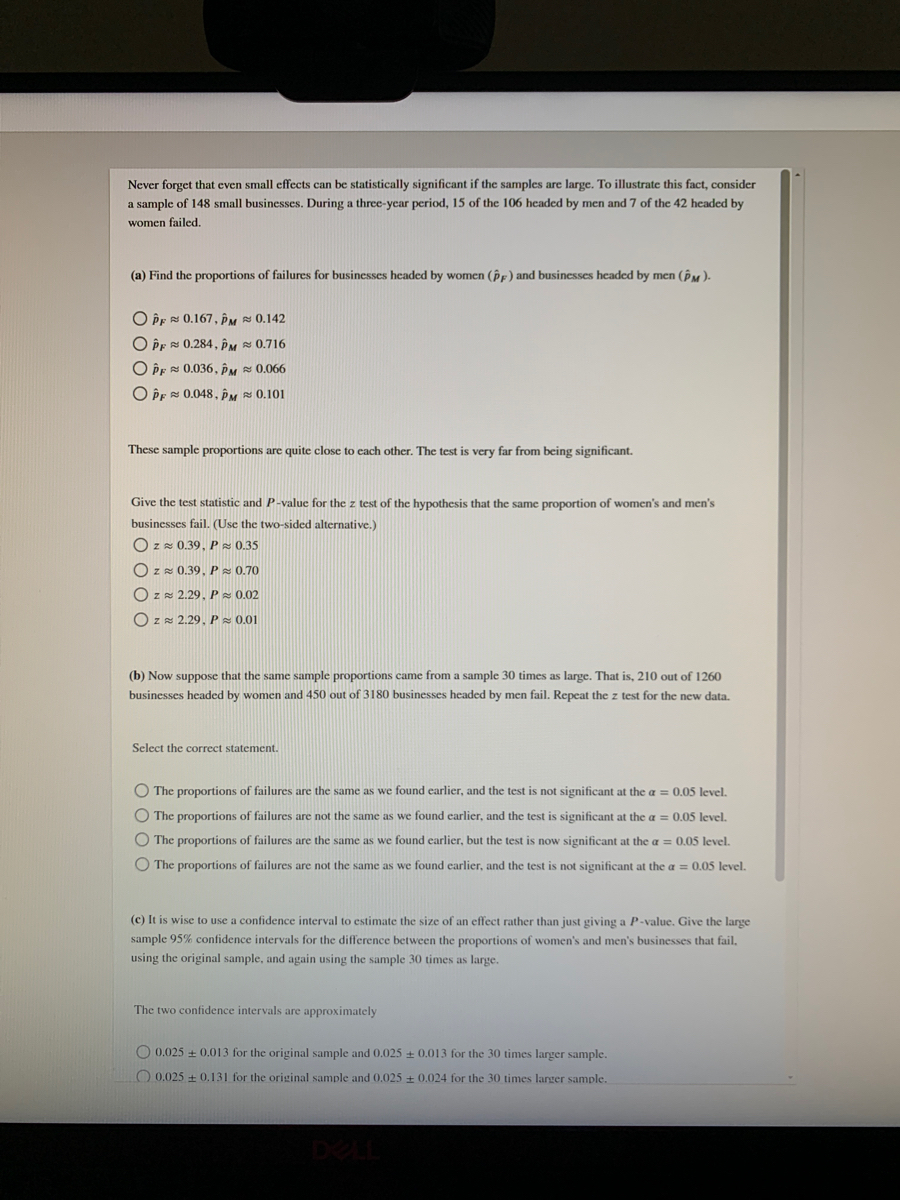
Extracted text: Never forget that even small effects can be statistically significant if the samples are large. To illustrate this fact, consider a sample of 148 small businesses. During a three-year period, 15 of the 106 headed by men and 7 of the 42 headed by women failed. (a) Find the proportions of failures for businesses headed by women (PF) and businesses headed by men (PM)- O Pr 0.167, PM 0,142 O PE 0.284, PM 0.716 O PE 0.036, ÊM 0.066 O PE 0.048, PM 0.101 These sample proportions are quite close to cach other. The test is very far from bcing significant. Give the test statistic and P-value for the z test of the hypothesis that the same proportion of women's and men's businesses fail. (Use the two-sided alternative.) Ozz 0.39, P 0.35 O zz 0.39, P 0.70 O z= 2.29, P = 0.02 O zz 2.29. P z 0.01 (b) Now suppose that the same sample proportions came from a sample 30 times as large. That is, 210 out of 1260 businesses headed by women and 450 out of 3180 businesses headed by men fail. Repeat the z test for the new data. Select the correct statement. O The proportions of failures are the same as we found earlier, and the test is not significant at the a = 0.05 level. O The proportions of failures are not the same as we found carlier, and the test is significant at the a = 0.05 level. O The proportions of failures are the same as we found earlier, but the test is now significant at the a = 0.05 level. O The proportions of failures are not the same as we found carlier, and the test is not significant at the a = 0.05 level. (c) It is wise to use a confidence interval to estimate the size of an effect rather than just giving a P-value. Give the large sample 95% confidence intervals for the difference between the proportions of women's and men's businesses that fail, using the original sample, and again using the sample 30 times as large. The two confidence intervals are approximately O 0.025 + 0.013 for the original sample and 0.025 0.013 for the 30 times larger sample. O 0.025 + 0.131 for the original sample and0.025 0.024 for the 30 times larger sample.
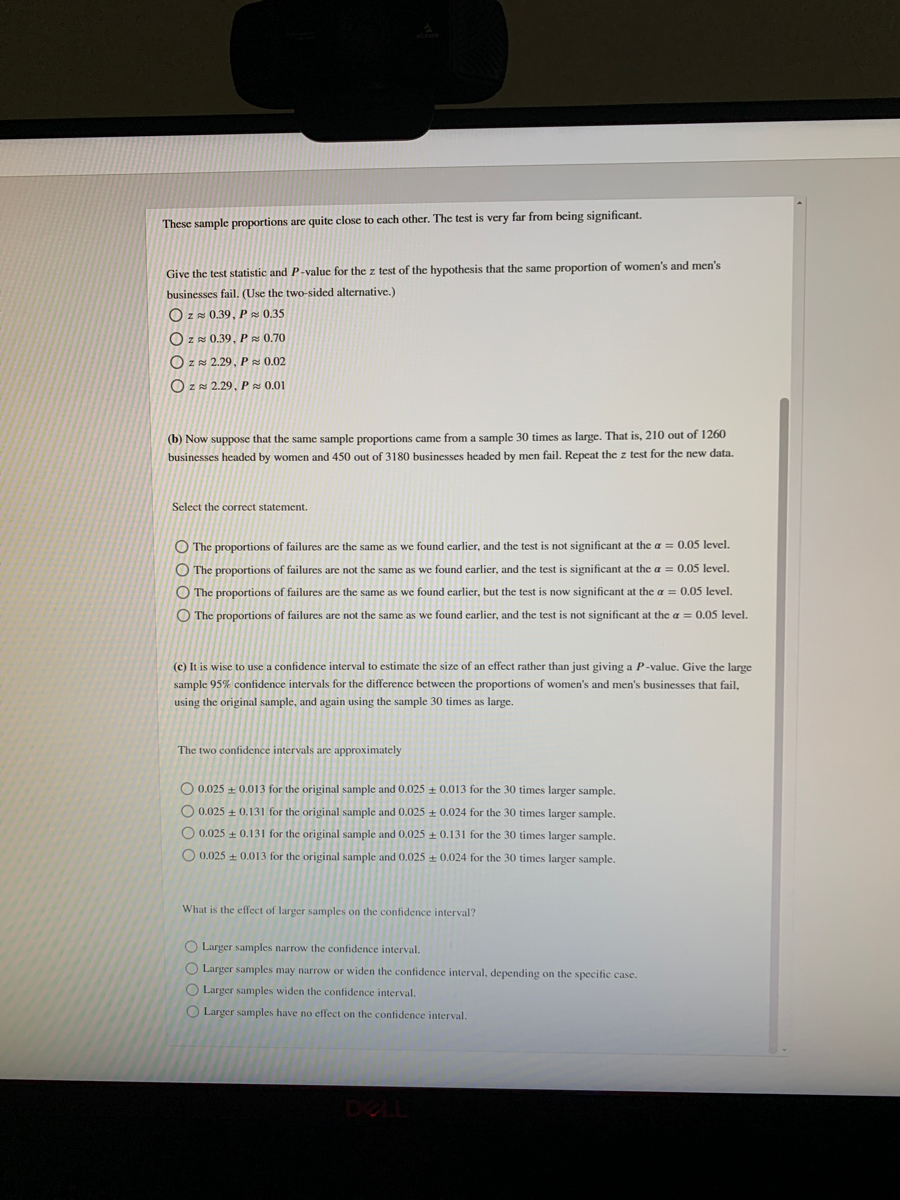
Extracted text: These sample proportions are quite close to cach other. The test is very far from being significant. Give the test statistic and P-value for the z test of the hypothesis that the same proportion of women's and men's businesses fail. (Use the two-sided alternative.) O z 0.39, P & 0.35 O Z 0.39, P 0.70 O ZN 2.29, P z 0.02 O ZN 2.29, P 0.01 (b) Now suppose that the same sample proportions came from a sample 30 times as large. That is, 210 out of 1260 businesses headed by women and 450 out of 3180 businesses headed by men fail. Repeat the z test for the new data. Select the correct statement. O The proportions of failures are the same as we found earlier, and the test is not significant at the a = 0.05 level. O The proportions of failures are not the same as we found earlier, and the test is significant at the a = 0,05 level. O The proportions of failures are the same as we found carlier, but the test is now significant at the a = 0.05 level. O The proportions of failures are not the same as we found carlier, and the test is not significant at the a = 0.05 level. (c) It is wise to use a confidence interval to estimate the size of an effect rather than just giving a P-value. Give the large sample 95% confidence intervals for the difference between the proportions of women's and men's businesses that fail, using the original sample, and again using the sample 30 times as large. The two confidence intervals are approximately O 0.025 + 0.013 for the original sample and 0.025 + 0.013 for the 30 times larger sample. O 0.025 + 0.131 for the original sample and 0.025 + 0.024 for the 30 times larger sample. O 0.025 + 0.131 for the original sample and 0.025 + 0.131 for the 30 times larger sample. O 0.025 + 0.013 for the original sample and 0.025 0.024 for the 30 times larger sample. What is the effect of larger samples on the confidence interval? O Larger samples narrow the confidence interval. O Larger samples may narrow or widen the confidence interval, depending on the specific case. O Larger samples widen the confidence interval. O Larger samples have no effect on the confidence interval. DELL