Multiple Regression, Confidence Intervals, Reliability of Cost Formulas
Randy Harris, controller, has been given the charge to implement an advanced cost management system. As part of this process, he needs to identify activity drivers for the activities of the firm. During the past four months, Randy has spent considerable effort identifying activities, their associated costs, and possible drivers for the activities' costs.
Initially, Randy made his selections based on his own judgment using his experience and input from employees who perform the activities. Later, he used regression analysis to confirm his judgment. Randy prefers to use one driver per activity, provided that anR
2 of at least 80 percent can be produced. Otherwise, multiple drivers will be used, based on evidence provided by multiple regression analysis. For example, the activity of inspecting finished goods produced anR
2 of less than 80 percent for any single activity driver. Randy believes, however, that a satisfactory cost formula can be developed using two activity drivers: the number of batches and the number of inspection hours. Data collected for a 14-month period are as follows:
Inspection Costs
|
Hours of Inspection
|
Number of Batches
|
| $17,689 | | 100 | | 10 |
| 18,350 | | 120 | | 20 |
| 13,125 | | 60 | | 15 |
| 28,000 | | 320 | | 30 |
| 30,560 | | 240 | | 25 |
| 31,755 | | 200 | | 40 |
| 40,750 | | 280 | | 35 |
| 29,500 | | 230 | | 22 |
| 47,570 | | 350 | | 50 |
| 36,740 | | 270 | | 45 |
| 43,500 | | 350 | | 38 |
| 26,780 | | 200 | | 18 |
| 28,500 | | 140 | | 28 |
| 17,000 | | 160 | | 14 |
1.Calculate the cost formula for inspection costs using the two drivers, inspection hours and number of batches. In the formula, round your answer for the intercept to the nearest whole number and round theX variables 1 and 2 to the nearest cent. WhereX
1 = hours of inspection, andX
2 = number of batches.
Y = $fill in the blank 1 + $fill in the blank 2X
1 + $fill in the blank 3X
2
Are both activity drivers useful?
Yes
What is the adjustedR
2? Round to the nearest whole percent.
fill in the blank
%
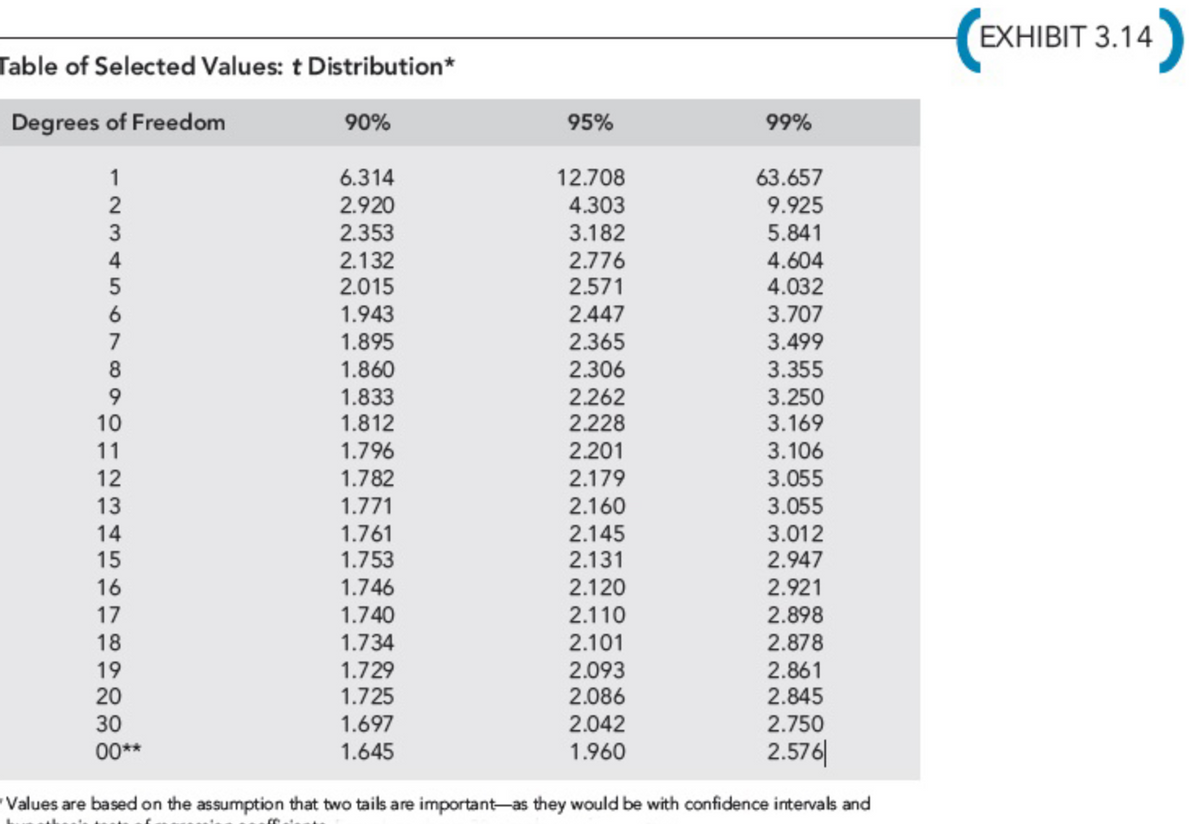
2.Using the formula developed in Requirement 1, calculate the inspection cost when 300 inspection hours are used and 30 batches are produced. Prepare a 90 percent confidence interval for this prediction. (Refer to Exhibit 3.14). In your computations, roundX
1 andX
2 to 2 decimals, round intercept,Yf
and the standard error to the nearest dollar and roundt-values to three decimals. Enter the final answers rounded to the nearest dollar.
Y = $fill in the blank 6
$fill in the blank 7 ≤Yf
≤ $fill in the blank 8
Extracted text: EXHIBIT 3.14 Table of Selected Values: t Distribution* Degrees of Freedom 90% 95% 99% 6.314 2.920 1 12.708 63.657 2 4.303 9.925 3 2.353 3.182 5.841 4 2.132 2.776 4.604 2.015 2.571 4.032 6 1.943 2.447 3.707 1.895 1.860 7 2.365 3.499 2.306 3.355 1.833 1.812 9. 2.262 3.250 10 2.228 3.169 11 1.796 2.201 3.106 12 1.782 2.179 3.055 2.160 2.145 13 1.771 3.055 14 1.761 3.012 15 1.753 2.131 2.947 2.921 2.898 16 1.746 2.120 17 1.740 2.110 1.734 1.729 1.725 18 2.101 2.878 2.093 2.086 2.861 2.845 19 20 30 00** 2.042 1.960 1.697 2.750 1.645 2.576| Values are based on the assumption that two tails are important-as they would be with confidence intervals and