Let(A,B,C) be a triangle in A2. Let M,N,P bethree points respectively on the lines BC,CA, and AB, of bary centric coordinates (0,m′,m′′),(n,0,n′′), and (p,p′,0),w.r.t. the affine frame (A,B,C).
(a) Assuming that M=C,N=A, and P=B,i.e., m′n′′p = 0, show that
(b)Prove Menelaus’s theorem: The points M,N, Pare collinear iff
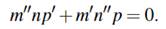
When M=C,N=A, and P=B, this is equivalent to
(c)Prove Ceva’s theorem: The lines AM,BN, CP have a unique intersection point or are parallel iff
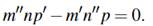
When M = C,N = A, and P = B, this is equivalent to