Let x, y, and z be real numbers. Prove the following.
(a) − (− x) = x.
(b) (− x) ⋅ y = − (x y) and (− x) ⋅ (− y) = x y.
(c) If x ≠ 0, then (1/x) ≠ 0 and 1/(1/x) = x.
(d) If x ⋅ z = y ⋅ z and z ≠ 0, then x = y.
(e) If x ≠ 0, then x2
> 0.
(f ) 0 <>
(g) If x > 1, then x2
> x.
(h) If 0 <><>2
( i ) If x > 0, then 1/x > 0. If x <>
( j ) If 0 <><><>
(k) If x y > 0, then either ( i ) x > 0 and y > 0, or ( ii ) x <>
( l ) For each n ∈ N, if 0 <><>n
n.
(m) If 0 <><>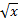
 .
.