Let us consider the population of the United States22 between the years 1800 and 1900. The annual growth rate can be estimated to be a =0.03: Assume that we have an exponential growth model and let r...

Let us consider the population of the United States22 between the years 1800 and 1900. The annual growth rate can be estimated to be a =0.03:

Assume that we have an exponential growth model and let r₀
= 5:3: Here t =0 corresponds to the year 1800: We want to estimate the population until 1900; i.e., we consider t between 0 and 100: Note that we count the population in millions, i.e., in the year 1800 approximately 5.3 million people lived in the United States.²³

(a)    Explain that an exponential growth model can be written in the form

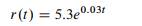
where t ranges from 0 to 100

(b)   We want to plot this solution and therefore we want t to go from 1800 to 1900. Show that we can define

(c)    Write a computer program to plot r(t ) for 1800 ≤ t ≤ 1900: In the same plot you should include the actual population given in the table below. Year Population (in millions)

(d) Use the model above to predict r(1980). The correct²⁴
number is about 226.5 million.

 (e) Use a logistic model with r₀
= 5.3 and a = 0.03. Plot the solutions for some values of the carrying capacity. Can you find a value of R such that the logistic model matches the data in the table better than the exponential model did? Furthermore, use your best value of R to estimate r(1980) Discuss how that relates to the actual figure.