Please provide unique solution. Thanks

Extracted text: Kiti laijlla| < (ei+j="" lai,j)|x;|="" using="" (2).="" hints:="" •="" remember="" that,="" a="" matrix="" a="" is="" invertible="" if="" the="" only="" solution="" to="" ax="0" is="" the="" 0="" vector,="" i.e.="" x="0." •="" suppose,="" for="" a="" ddm="" (diagonally="" dominated="" matrix),="" there="" exists="" a="" non-zero="" solution="" to="" x1="" x2="" ax="0." since="" x="Let's" say,="" xi="" has="" the="" greatest="" magnitude="" here="" which="" means="" |x;|=""> |xj| for all j # i ...(2). • Since, Ax = 0, we must have, ai,1X1+ ai,2x2 + · · · + ai.nxn = 0 for the i'th row. In other words, ai,1X1 + ai,2x2 + · · ·+ ai,i–1Xi-1+ai,i+1Xi+1+ • · · + ai,nXn = –aj,iXi or, |ai,121 + ai,2x2 + + a;,i-1Xi-1+a¿,i+1Xj+1+ . . + ai,n&n| = |ai,¿X¡| But we will prove that, this is not possible when x is non-zero. So, we have proved that, |Eitj aijaj| < |ai,ixi|="" explanation:="" |eitj="" ai,ja;|="">< eiti="" lai,j*;|="" because="" |æ="" +="" y|="">< |x|="" +="" \y|="" for="" all="" real="" numbers="" x,="" y,="" z.="" ¿="" lai.jª="" j|="Eitj" lai.j||xj|="" because="" |æy|="|c||y|" for="" all="" real="" a,="" y.="" (eitj="" laij)|#;|="">< |a;,a||x:|="" using="">
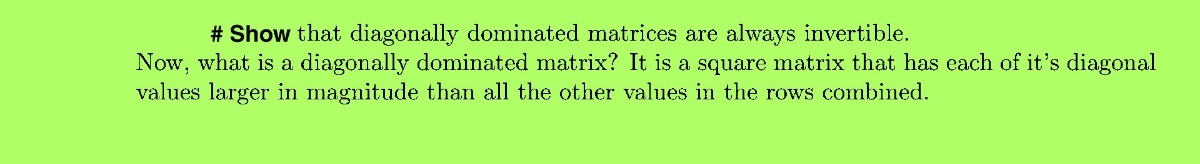
Extracted text: # Show that diagonally dominated matrices are always invertible. Now, what is a diagonally dominated matrix? It is a square matrix that has each of it's diagonal values larger in magnitude than all the other values in the rows combined.