Is a basketball player's ability to make free throws different when they get their own rebound or when someone else gets their rebound for them? This is what student researchers wanted to explore. The researchers used students (20 females and 20 males) taking a college physical education class as their subjects. The students each attempted 10 shots from the free throw line where they had to get their own rebound and 10 shots where someone else got their rebound and passed the ball back to them while they stayed on the free throw line. They randomly determined the order that they took these shots, with some getting their own rebounds first and some having someone else get the rebounds first. Here are the hypotheses in the picture:
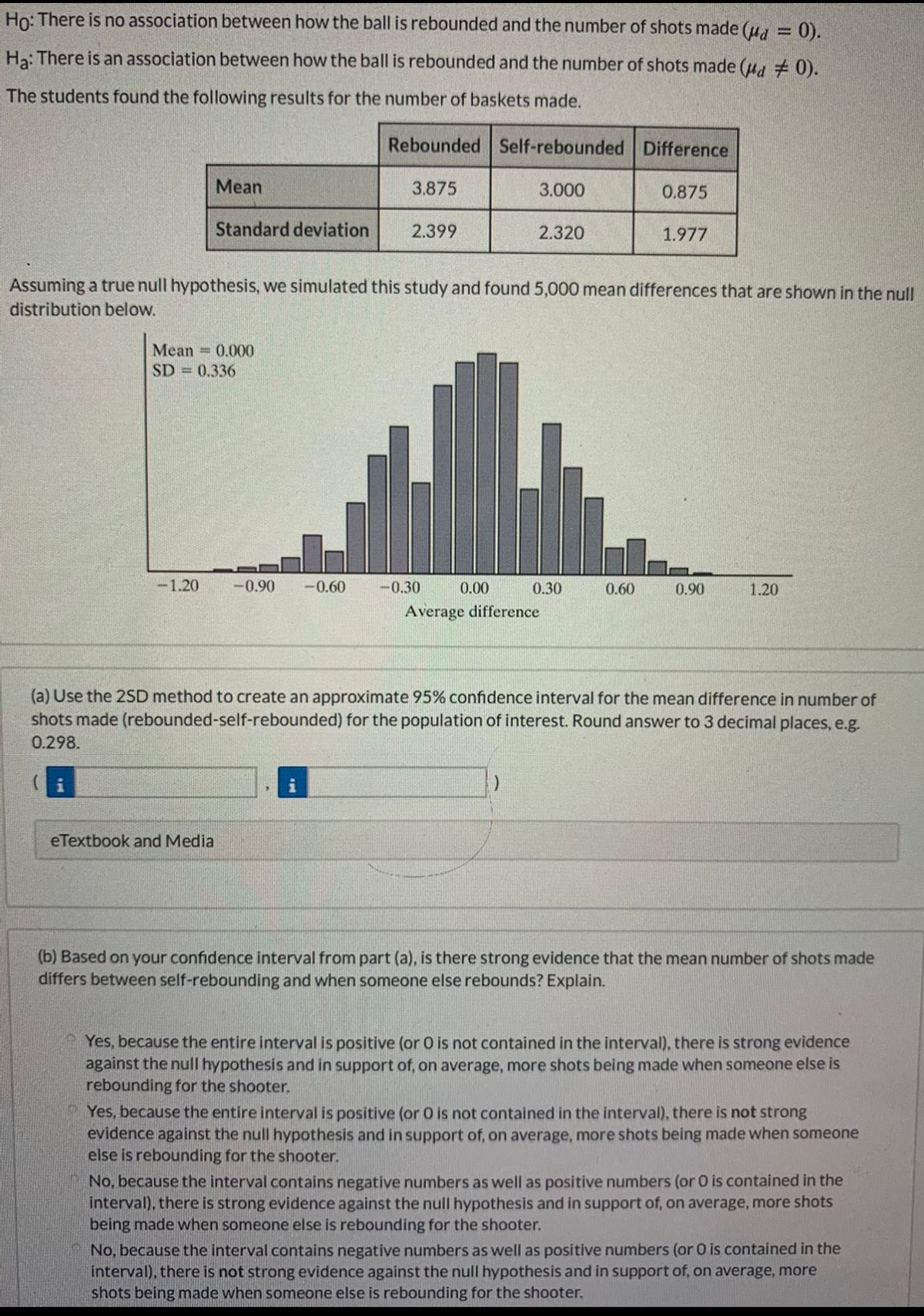
Extracted text: Ho: There is no association between how the ball is rebounded and the number of shots made (u, = 0). Ha: There is an association between how the ball is rebounded and the number of shots made (u, 0). The students found the following results for the number of baskets made. Rebounded Self-rebounded Difference Mean 3.875 3.000 0.875 Standard deviation 2.399 2.320 1.977 Assuming a true null hypothesis, we simulated this study and found 5,000 mean differences that are shown in the null distribution below. Mean = 0.000 SD = 0.336 -1.20 -0.90 -0.60 -0.30 0.00 0.30 0.60 0.90 1.20 Average difference (a) Use the 2SD method to create an approximate 95% confidence interval for the mean difference in number of shots made (rebounded-self-rebounded) for the population of interest. Round answer to 3 decimal places, e.g. 0.298. eTextbook and Media (b) Based on your confidence interval from part (a), is there strong evidence that the mean number of shots made differs between self-rebounding and when someone else rebounds? Explain. Yes, because the entire interval is positive (or O is not contained in the interval), there is strong evidence against the null hypothesis and in support of, on average, more shots being made when someone else is rebounding for the shooter. Yes, because the entire interval is positive (or 0 is not contained in the interval), there is not strong evidence against the null hypothesis and in support of, on average, more shots being made when someone else is rebounding for the shooter. No, because the interval contains negative numbers as well as positive numbers (or 0 is contained in the interval), there is strong evidence against the null hypothesis and in support of, on average, more shots being made when someone else is rebounding for the shooter. No, because the interval contains negative numbers as well as positive numbers (or 0 is contained in the interval), there is not strong evidence against the null hypothesis and in support of, on average, more shots being made when someone else is rebounding for the shooter.