Internet addiction has been described as excessive and uncontrolled Internet use. The authors of a research article used a score designed to measure the extent and severity of Internet addiction in a study of 837 male and 874 female sixth-grade students in China. Internet Addiction was measured using Young's Internet Addiction Diagnostic Test. The lowest possible score on this test is zero, and higher scores indicate higher levels of Internet addiction. For the sample of males, the mean Internet Addiction score was 1.51 and the standard deviation was 2.02. For the sample of females, the mean was 1.01 and the standard deviation was 1.67. For purposes of this exercise, you can assume that it is reasonable to regard these two samples as representative of the population of male Chinese sixth-grade students and the population of female Chinese sixth grade students, respectively.
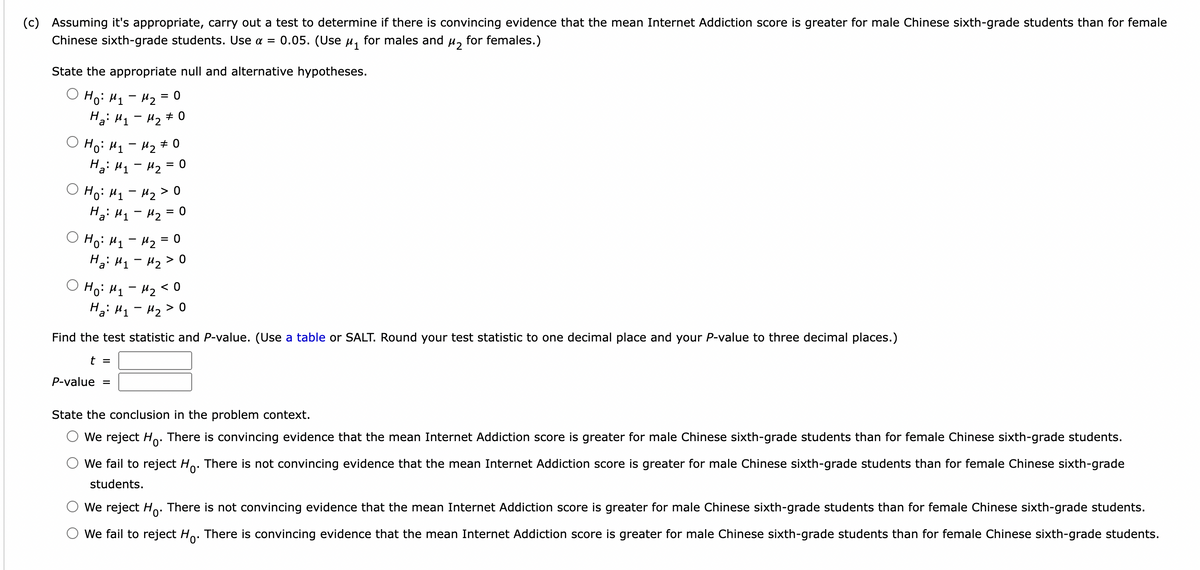
Extracted text: (c) Assuming it's appropriate, carry out a test to determine if there is convincing evidence that the mean Internet Addiction score is greater for male Chinese sixth-grade students than for female Chinese sixth-grade students. Use a = 0.05. (Use u, for males and for females.) State the appropriate null and alternative hypotheses. Hoi Hy- Mz = 0 Hai H1 - H2 # 0 O Ho: H1 - 42 + o H: H1 - H2 = 0 O Ho: H1 - 42 > 0 Hai H1- Hz = O Ho: H1 - 42 = 0 H: H1 - H2 > 0 O Ho: H1 - 42 < 0="" hai="" h1-="" hz="">0 a Find the test statistic and P-value. (Use a table or SALT. Round your test statistic to one decimal place and your P-value to three decimal places.) t = P-value = State the conclusion in the problem context. We reject Ho. There is convincing evidence that the mean Internet Addiction score is greater for male Chinese sixth-grade students than for female Chinese sixth-grade students. We fail to reject Ho. There is not convincing evidence that the mean Internet Addiction score is greater for male Chinese sixth-grade students than for female Chinese sixth-grade students. We reject Ho. There is not convincing evidence that the mean Internet Addiction score is greater for male Chinese sixth-grade students than for female Chinese sixth-grade students. We fail to reject Ho. There is convincing evidence that the mean Internet Addiction score is greater for male Chinese sixth-grade students than for female Chinese sixth-grade students.

Extracted text: Internet addiction has been described as excessive and uncontrolled Internet use. The authors of a research article used a score designed to measure the extent and severity of Internet addiction in a study of 837 male and 874 female sixth-grade students in China. Internet Addiction was measured using Young's Internet Addiction Diagnostic Test. The lowest possible score on this test is zero, and higher scores indicate higher levels of Internet addiction. For the sample of males, the mean Internet Addiction score was 1.51 and the standard deviation was 2.02. For the sample of females, the mean was 1.01 and the standard deviation was 1.67. For purposes of this exercise, you can assume that it is reasonable to regard these two samples as representative of the population of male Chinese sixth-grade students and the population of female Chinese sixth grade students, respectively. In USE SALT (a) The standard deviation is greater than the mean for each of these samples. Explain why it is not reasonable to think that the distribution of Internet Addiction scores would be approximately normal for either the population of male Chinese sixth-grade students or the population of female Chinese sixth-grade students. (Round your numeric values to two decimal place.) If the distributions were both approximately normal, then % of the male Internet Addiction scores would be negative, and % of the female Internet Addiction scores would be negative. Assuming that the scores must be positive, these percentages are too large to make it reasonable to believe that the distributions are approximately normal. (b) Given your response to part (a), would it be appropriate to use the two-sample t test to test the null hypothesis that there is no difference in the mean Internet Addiction score for male Chinese sixth-grade students and female Chinese sixth-grade students? Explain why or why not. It would not be appropriate because the distributions of Internet Addiction scores are not approximately normal. It would be appropriate because the sample sizes are both much larger than 30, so the central limit theorem states that the sampling distributions of sample means are approximately normal. It would not be appropriate because the sample sizes are both much larger than 30, so the central limit theorem states that the sampling distributions of sample means are not approximately normal. It would be appropriate because the distributions of Internet Addiction scores are approximately normal.