Instead of the 75 mm thick wooden plate in the previous exercise, a very long, square wooden trunk, with a side length of 75 mm is to be dried. The mass fraction of water and the diffusion coefficient are the same as in the previous question: ξAα = 0.218, ξAS = 0.065, D = 1.2 · 10−9 m2/s. How long will it take for the mass fraction of water in the core of the trunk to fall to ξA(x = 0, y = 0) = 0.08?
In a spray absorber, a waste gas containing ammonia will be purified with water. The waste gas and water droplets flow countercurrent to each other as shown in Fig. 2.72. The saturated concentration of ammonia (substance A) for a temperature of 10 ◦C of the spray water and a pressure of 0.11 MPa appears at the surface of the falling water droplets. The mass fraction of ammonia at saturation is ξA0 = 0.4. The following mass flow rates and mass fractions are given: water feed M˙ W = 2.3 kg/s, waste gas feed M˙ Gi = 4.4 kg/s, mass fraction of ammonia in the waste gas feed ξG Ai = 0.12; this should be reduced to a value of ξG Ao = 0.006 in the waste gas exit stream; the mass fraction of ammonia in the water outlet is allowed to reach ξL Ao = 0.24. The fraction of water in the waste gas is negligible.
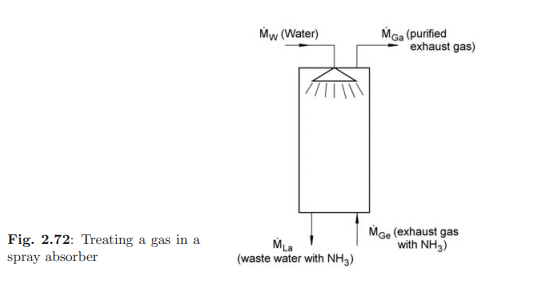
a) What are the mass flow rates M˙ Go of the waste gas, M˙ Lo of the waste water and what mass flow rate of water M˙ W has to be fed into the absorber?
b) After what period of time has the average mass fraction of NH3 in the water outlet stream increased to ξL Ao = 0.24? The diameter of the water droplets is 3 mm and the diffusion coefficient of NH3 in H2O is D = 1.5 · 10−9 m2/s.
c) How high is the spray absorber if the water droplets are to fall through the rising waste gas with a velocity of w = 0.1 m/s?