In this problem, assume that the distribution of differences is approximately normal.
Note: For degrees of freedom
d.f. not in the Student's
t
table, use the closest
d.f. that is
smaller. In some situations, this choice of
d.f. may increase the
P-value by a small amount and therefore produce a slightly more "conservative" answer.
In the following data pairs,
A
represents birth rate and
B
represents death rate per 1000 resident population. The data are paired by counties in the Midwest. A random sample of 16 counties gave the following information.
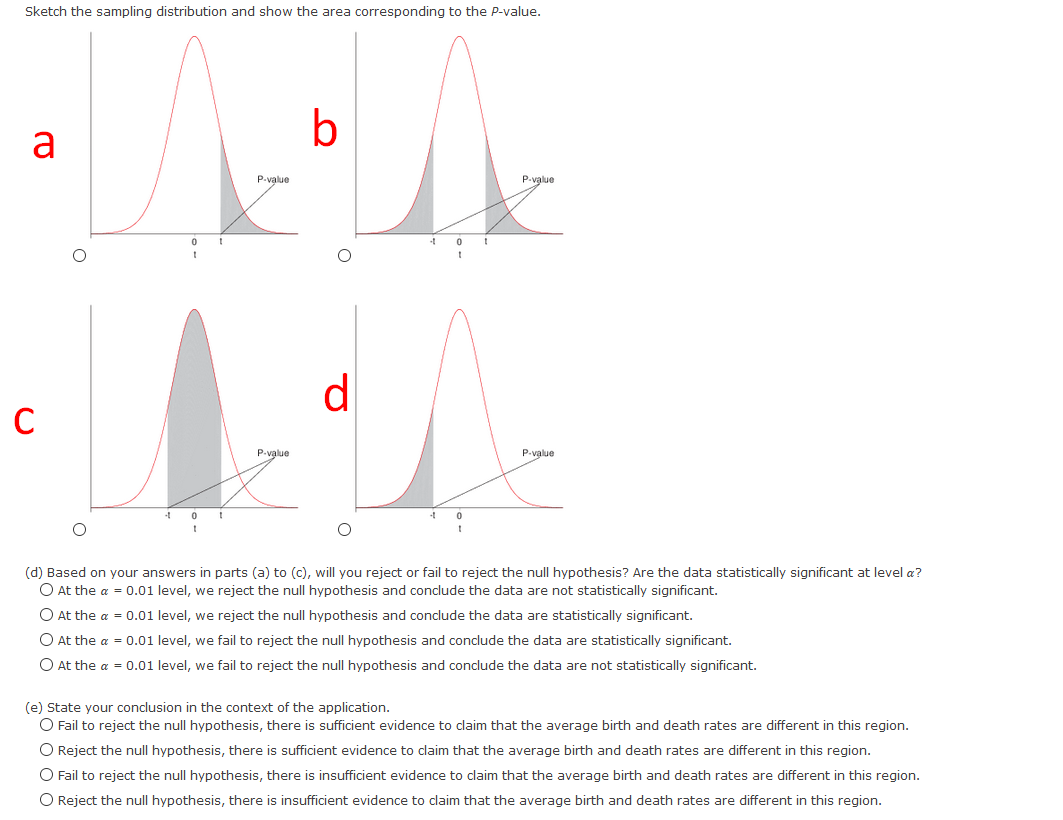
Extracted text: Sketch the sampling distribution and show the area corresponding to the P-value. a P-value P-value d P-value P-value (d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis? Are the data statistically significant at level a? O At the a = 0.01 level, we reject the null hypothesis and conclude the data are not statistically significant. O At the a = 0.01 level, we reject the null hypothesis and conclude the data are statistically significant. O At the a = 0.01 level, we fail to reject the null hypothesis and conclude the data are statistically significant. O At the a = 0.01 level, we fail to reject the null hypothesis and conclude the data are not statistically significant. (e) State your conclusion in the context of the application. O Fail to reject the null hypothesis, there is sufficient evidence to claim that the average birth and death rates are different in this region. O Reject the null hypothesis, there is sufficient evidence to claim that the average birth and death rates are different in this region. O Fail to reject the null hypothesis, there is insufficient evidence to claim that the average birth and death rates are different in this region. O Reject the null hypothesis, there is insufficient evidence to claim that the average birth and death rates are different in this region.
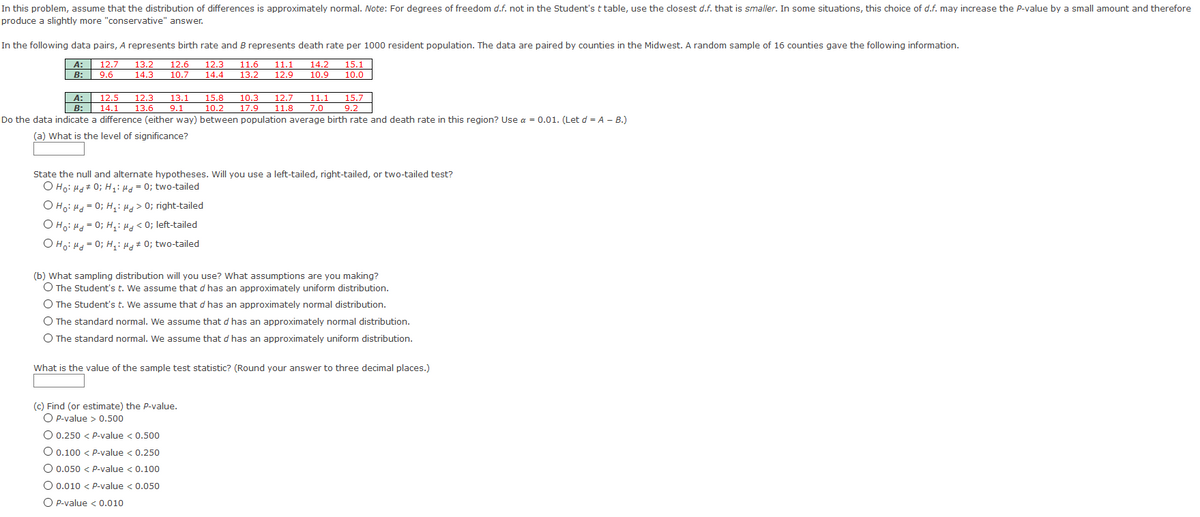
0; right-tailed O Ho: H = 0; H,: H < 0;="" left-tailed="" o="" ho:="" h="0;" h,:="" hg#="" 0;="" two-tailed="" (b)="" what="" sampling="" distribution="" will="" you="" use?="" what="" assumptions="" are="" you="" making?="" o="" the="" student's="" t.="" we="" assume="" that="" d="" has="" an="" approximately="" uniform="" distribution.="" o="" the="" student's="" t.="" we="" assume="" that="" d="" has="" an="" approximately="" normal="" distribution.="" o="" the="" standard="" normal.="" we="" assume="" that="" d="" has="" an="" approximately="" normal="" distribution.="" o="" the="" standard="" normal.="" we="" assume="" that="" d="" has="" an="" approximately="" uniform="" distribution.="" what="" is="" the="" value="" of="" the="" sample="" test="" statistic?="" (round="" your="" answer="" to="" three="" decimal="" places.)="" (c)="" find="" (or="" estimate)="" the="" pp-value.="" o="" p-value=""> 0.500 O 0.250 < p-value="">< 0.500="" o="" 0.100="">< p-value="">< 0.250="" o="" 0.050="">< p-value="">< 0.100="" o="" 0.010="">< p-value="">< 0.050="" o="" p-value="">< 0.010="" "/="">
Extracted text: In this problem, assume that the distribution of differences is approximately normal. Note: For degrees of freedom d.f. not in the Student's t table, use the closest d.f. that is smaller. In some situations, this choice of d.f. may increase the P-value by a small amount and therefore produce a slightly more "conservative" answer. In the following data pairs, A represents birth rate and B represents death rate per 1000 resident population. The data are paired by counties in the Midwest. A random sample of 16 counties gave the following information. A: 12.7 13.2 12.6 12.3 11.6 11.1 14.2 15.1 B: 9.6 14.3 10.7 14.4 13.2 12.9 10.9 10.0 12.3 A: B: 12.5 13.1 15.8 10.3 12.7 11.1 15.7 14.1 13.6 9.1 10.2 17.9 11.8 7.0 9.2 Do the data indicate a difference (either way) between population average birth rate and death rate in this region? Use a = 0.01. (Let d = A – B.) (a) What is the level of significance? State the null and alternate hypotheses. Will you use a left-tailed, right-tailed, or two-tailed test? O Ho: Hd# 0; H;:H = 0; two-tailed O Ho: Hd = 0; H:> 0; right-tailed O Ho: H = 0; H,: H < 0;="" left-tailed="" o="" ho:="" h="0;" h,:="" hg#="" 0;="" two-tailed="" (b)="" what="" sampling="" distribution="" will="" you="" use?="" what="" assumptions="" are="" you="" making?="" o="" the="" student's="" t.="" we="" assume="" that="" d="" has="" an="" approximately="" uniform="" distribution.="" o="" the="" student's="" t.="" we="" assume="" that="" d="" has="" an="" approximately="" normal="" distribution.="" o="" the="" standard="" normal.="" we="" assume="" that="" d="" has="" an="" approximately="" normal="" distribution.="" o="" the="" standard="" normal.="" we="" assume="" that="" d="" has="" an="" approximately="" uniform="" distribution.="" what="" is="" the="" value="" of="" the="" sample="" test="" statistic?="" (round="" your="" answer="" to="" three="" decimal="" places.)="" (c)="" find="" (or="" estimate)="" the="" pp-value.="" o="" p-value=""> 0.500 O 0.250 < p-value="">< 0.500="" o="" 0.100="">< p-value="">< 0.250="" o="" 0.050="">< p-value="">< 0.100="" o="" 0.010="">< p-value="">< 0.050="" o="" p-value="">< 0.010>