In the peak-load pricing model in Example 7.4, we assumed that the capacity level is a decision variable. Assume now that capacity has already been set at 30 kwh. (Note that the cost of capacity is now a sunk cost, so it is irrelevant to the decision problem.) Change the model appropriately and run Solver. Then use SolverTable to see how sensitive the optimal solution is to the capacity level, letting it vary over some relevant range. Does it appear that the optimal prices are set so that demand always equals capacity for at least one of the two periods of the day?
EXAMPLE 7.4 PEAK-LOAD PRICING AT FLORIDA POWER AND LIGHT
Florida Power and Light (FPL) faces demands during both peak-load and off-peak times. FPL must determine the price per kilowatt hour (kwh) to charge during both peak-load and off-peak periods. The daily demand for power during each period (in kwh) is related to price as follows:
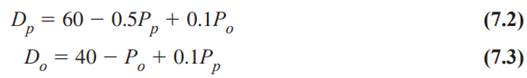
Here, Dp and Pp are demand and price during peak-load times, whereas Do and Po are demand and price during off-peak times. Note that these are linear demand functions, not the constant elasticity demand functions from the previous examples. (We do this for the sake of variety. The model would not differ substantially with constant elasticity demand functions.) Also, note from the signs of the coefficients that an increase in the peak-load price decreases the demand for power during the peak-load period but increases the demand for power during the off-peak period. Similarly, an increase in the price for the off-peak period decreases the demand for the off-peak period but increases the demand for the peak-load period. In economic terms, this implies that peak-load power and off-peak power are substitutes for one another. In addition, it costs FPL $10 per day to maintain 1 kwh of capacity. The company wants to determine a pricing strategy and a capacity level that maximize its daily profit.
Objective To use a nonlinear model to determine prices and capacity when there are two different daily usage patterns: peak load and off peak.
WHERE DO THE NUMBERS COME FROM? As usual, a cost accountant should be able to estimate the unit cost of capacity. The real difficulty here is estimating the demand functions in Equations (7.2) and (7.3). This requires either sufficient historical data on prices and demands (for both peak-load and off-peak periods) or educated guesses from management.