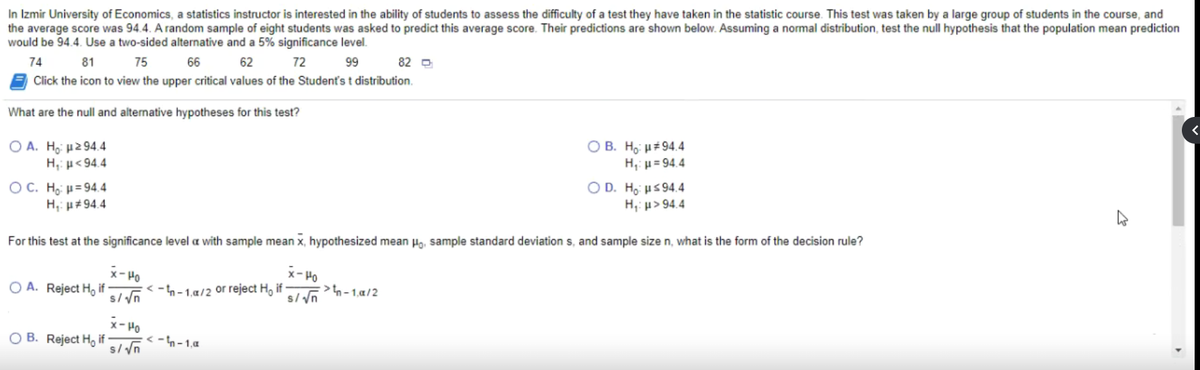
Extracted text: In Izmir University of Economics, a statistics instructor is interested in the ability of students to assess the difficulty of a test they have taken in the statistic course. This test was taken by a large group of students in the course, and the average score was 94.4. A random sample of eight students was asked to predict this average score. Their predictions are shown below. Assuming a normal distribution, test the null hypothesis that the population mean prediction would be 94.4. Use a two-sided alternative and a 5% significance level. 74 81 75 66 62 72 99 82 D Click the icon to view the upper critical values of the Student's t distribution. What are the null and alternative hypotheses for this test? Ο Α. H μ2 94.4 H,: µ<94.4 ов.="" на="" и#94.4="" h,="" µ="94.4" oc.="" họi="" µ="94.4" h,:="" p#94.4="" o="" d.="" h,="" us="" 94.4="" h,:="" p=""> 94.4 For this test at the significance level a with sample mean x, hypothesized mean Hg, sample standard deviation s, and sample size n, what is the form of the decision rule? x- Ho >n -1,a/2 x- Ho O A. Reject H, if s//n -h-1.a/2 or reject H, if x- Ho O B. Reject H, if < -n-="">
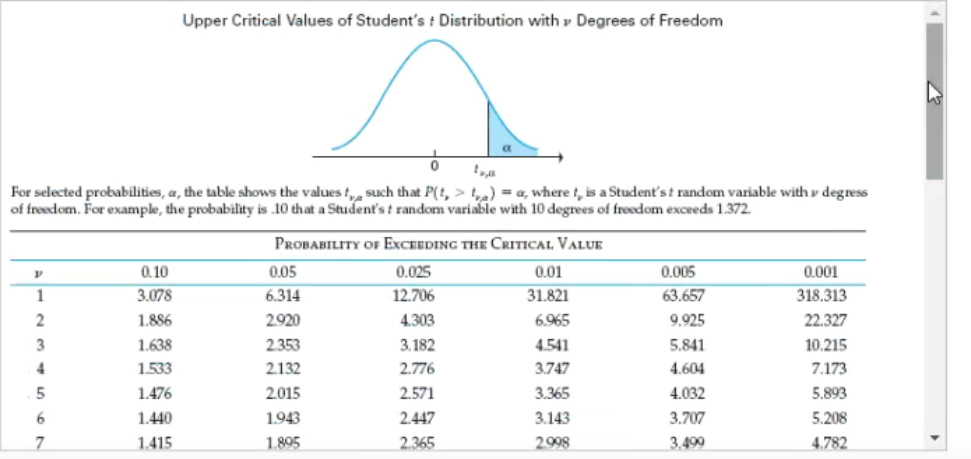
Extracted text: Upper Critical Values of Student's t Distribution with y Degrees of Freedom For selected probabilities, a, the table shows the values t such that P(t, > t) = a, where t, is a Student's t random variable with y degress of freedom. For example, the probability is 10 that a Student's t random variable with 10 degrees of freedom exceeds 1.372. PROBABILITY Or EXCEEDING THE CRITICAL VALUE 0.10 0.05 0.025 0.01 0.005 0.001 1 3.078 6.314 12.706 31.821 63.657 318.313 1.886 2920 4.303 6.965 9.925 22.327 3 1.638 2.353 3.182 4.541 5.841 10.215 1.533 2.132 2.776 3.747 4.604 7.173 1.476 2.015 2.571 3.365 4.032 5.893 1.440 1.943 2.447 3.143 3.707 5.208 7 1.415 1.895 2.365 2.998 3.499 4.782