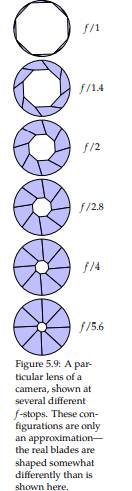
In a typical optical camera lens, the light that enters the lens (through the opening called the aperture) is controlled by a collection of movable blades that can be adjusted inward to narrow the area through which light can pass. (There are two effects of narrowing this opening: first, the amount of light entering the lens is reduced, darkening the resulting image; and, second, the depth of field—the range of distances from the lens at which objects are in focus in the image—increases.) Although some lenses allow continuous adjustment to their openings, many have a sequence of so-called stops: discrete steps by which the aperture narrows. (See Figure 5.9.) These steps are called f -stops (the “f” is short for “focal”), and they are denoted with some unusual notation that you’ll unwind in this exercise. The “fastest” f-stop for a lens measures the ratio of two numbers: the focal length of the lens divided by the diameter of the aperture of the lens. (For example, you might use a lens that’s 50mm long and that has a 25mm diameter, which yields an f-stop of 50mm/25mm = 2.) One can also “stop down” a lens from this fastest setting by adjusting the blades to shrink the diameter of the aperture, as described above. (For example, for the 50mm-long lens with a 25mm diameter, you might reduce the diameter to 12.5mm, which yields an f-stop of 50mm/12.5mm = 4.) f /1 f /1.4 f /2 f /2.8 f /4 f /5.6 Figure 5.9: A particular lens of a camera, shown at several different f-stops. These configurations are only an approximation— the real blades are shaped somewhat differently than is shown here. Consider a camera lens with a 50mm focal length, and let d0 := 50mm denote the diameter of the lens’s aperture diameter. “Stopping down” the lens by one step causes the lens’s aperture diameter to shrink by a factor of √1 2 —that is, the next-smaller aperture diameter for a diameter di is defined as

Give a closed-form expression for dn—that is, give a nonrecursive numerical expression whose value is equal to dn (where your expression involves only real numbers and the variable n). Prove your answer correct by
induction on n. Also give a closed-form expression for two further quantities:
• the “light-gathering” area (that is, the area of the aperture) of the lens when its diameter is set to dn.
• the f-stop fn of the lens when its diameter is set to dn. (Using your formula for fn, can you explain the f-stop names from Figure 5.9?)
