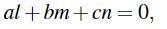(i) In the projective space RP3,a line D is determined by two distinct hyper-planes of equations
Where (α,β,γ,δ) and (α′,β′,γ′,δ′) are linearly independent. Prove that the equations of the two hyper planes defining D canal ways
Bew written either as
Where
 and either
and either
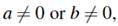
Or as
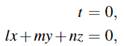
Where l=0,m=0,orn=0. In the first case, prove that D is also determined by the intersection of three hyper planes who se equations are of the form
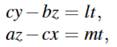
Bx – ay = nt,
Where the equation
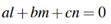
holds, and where a=0,b=0, or c=0. We can view (a,b,c,l,m,n) as homogeneous coordinates in RP5 associated with D. In the case where the equations of D are
We let (0,0,0,l,m,n) be the homogeneous scoord in at esassociated with D. Of course, al+bm+cn=0 holds. The homogeneous scoordinates (a,b,c,l,m,n) such that al+bm+cn=0 are called the Pl ucker coordinates of D.
(ii) Conversely, given some homogeneous coordinates (a,b,c,l,m,n) in RP5 satisfying the equation