Here we reformulate the multitaper-based simple linear regression model of Equation (409d) in standard vector/matrix notation (see, e.g., Weisberg, 2014), with the goal of verifying Equation (410b), which gives the variance of the OLS estimator
 of the power-law exponent α. Let Y be a column vector containing the responses
of the power-law exponent α. Let Y be a column vector containing the responses
 and let X be a matrix with two columns of predictors, the first column with elements all equal to unity, and the second, with elements equal to
and let X be a matrix with two columns of predictors, the first column with elements all equal to unity, and the second, with elements equal to
 as defined in Equation (409e).
as defined in Equation (409e).
(a) With
 being a two-dimensional column vector of regression coefficients whose second element is α, argue that
being a two-dimensional column vector of regression coefficients whose second element is α, argue that
 is equivalent to the model of Equation (409d), where is a column vector containing the error terms
is equivalent to the model of Equation (409d), where is a column vector containing the error terms
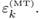
(b) A standard result says that the OLS estimator of
 (see, e.g., Weisberg, 2014). Show that the second element of βˆ is the multitaper-based OLS estimator ˆα (MT) of Equation (409e).
(see, e.g., Weisberg, 2014). Show that the second element of βˆ is the multitaper-based OLS estimator ˆα (MT) of Equation (409e).
(c) Taking the elements of the covariance matrix Σ for to be dictated by Equation (410a); noting that
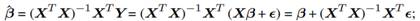
and evoking a standard result from the theory of multivariate RVs, namely, that the covariance matrix for Mis given by
 show that var
show that var is given by.
is given by.