
Group Names: Aimee Castro, Emely
Exploration 1: Finding a best-fitting function
The table below contains the average distance D from the sun for eight planets and their period P of revolution around the sun in years. The distances are measured in astronomical units (A.U.), where 1 A.U. is the average distance from the earth to the sun. For example, since Jupiter’s distance is 5.2 A.U., it’s distance from the sun is 5.2 times farther than the average distance of the earth from the sun. (Source: The Natural History of the Universe.)
Table 1: Data on Period vs Distance for the Eight Planets.
Planet
|
Distance D (A.U.)
|
Period P
|
Mercury
|
0.39
|
0.24
|
Venus
|
0.72
|
0.62
|
Earth
|
1
|
1
|
Mars
|
1.52
|
1.89
|
Jupiter
|
5.2
|
11.9
|
Saturn
|
9.54
|
29.5
|
Uranus
|
19.2
|
84.0
|
Neptune
|
30.1
|
164.8
|
We want to find a model that fits this set of data. Before we look at a graph, let’s first understand the data and its meaning.
Question 1:
In the table, the planets are ordered by their distance from the sun. What can you say about the periods for these planets? Do they increase as the distance from the sun increases, do they decrease or is it a mix? Can you explain the behavior you observe from the fact that the orbits are ovals around the sun?
As the periods for these planets increase the distance from the sun increases. By observing the fact that the orbits are ovals around the sun, the behavior may be explained that at some point the graph will increase and at others it will decrease.
A. Exploring Possible Types of Models
Task 1:
Copy the data for the variables into a Google Sheet document or an Excel workbook and graph them. Give your graph a title, and if you can, label the data points with the names of the planets. Copy the graph into this document.
By
Question 2:
Looking at the shape of the data, what type of functions might be appropriate as a model for how the period depends on the distance? Give at least two possibilities and explain why you selected those types of functions (make reference to the shape and other properties of these functions).
Based on the shape of the data, a polynomial function might be appropriate as a model for how the period depends on the distance. Another possible function for the data might be an exponential function as the model grows positively. We can eliminate log function, quadratic, and cubic because the function does not have an asymptote, it is not u-shaped or s-shaped.
B. Working with Specific Types of Models
Task 2:
We will now assume that the data follows a particular model and then determine parameters so that the model passes through the point for the planet Neptune, that is, the model fits exactly for Neptune. The three models you will fit are of the form P=c Dn, with n=1, 1.5, or 2 and c is the parameter value that we need to find to determine the specific model in each case.
For each value of n given in Table 2, do the tasks below.
Write down the formula for P for the particular value of n and write down the name of the type of function.
Use the data point for Neptune, D,P=(30.1, 164.8) to solve for the parameter value c. Round your answer to two decimal places. Enter the value into Table 2.
Write the model after you have substituted the value of c that you found in Table 2 below.
Use the model to predict the period of Pluto (which was removed from the list of planets in 2006), using that Pluto has a distance from the sun of 39.5 A.U you did for the predictions. Round your answer to one decimal place.
Enter the answers into Table 2 and show your work for parts 2 and 4 in the designated space below by either:
using Hypatia Create and typing in the derivations directly into this document into the space below; or
by writing it neatly on paper, scanning it in, and pasting into the space below; or
by writing it neatly on a tablet, taking a screen shot, and pasting into the space below.
To paste your work into the Google sheet, make sure your scan is a pgn format.










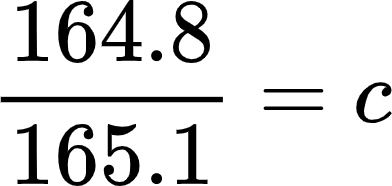


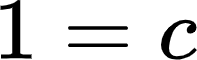








At this point, you should have filled in Table 2. Make sure to use proper math notation, such as writing
PD=2.45D3 for the formulas, not 2.45D^3.
Table 2: Summary of three different models for the planets that fit exactly at Neptune
n
|
Formula
|
Type of function
|
Value of c
|
Model
|
Period of Pluto
|
1
|

|
Exponential
|
5.48
|

|
216.46
|
1.5
|
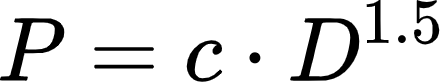
|
Exponential
|
1
|

|
215.10
|
2
|

|
Quadratic
|
0.18
|

|
280.85
|
Note that in Task 2 we were given the type of model, and therefore used only one point to find the one missing parameter c.
C. Comparing and Assessing the Three Types of Models
Task 3:
Visually assess which of the three models, which all fit the point for Neptune exactly, fits the data best overall. Paste the data values from Table 1 (only last two columns, and no headings) into Desmos. Then graph the three models you found above. Take a screenshot and paste it into this document, then add a legend that explains which graph belongs to which model. For example, you can write: The green graph corresponds to PD=…, the red one to PD=…, etc.



The purple graph corresponds to

The pink graph corresponds to

The green graphs corresponds to

Task 4:
Copy the data into a Google or Excel spreadsheet and follow the steps used in class for the fetal stature data to compute the sum or squared errors for each of the three models. Highlight the cells containing the SSE, then take a screenshot of the table of computed values together with the data and paste it here.
Task 5:
Compare the three model predictions for the period of Pluto with the actual period of 248.5 years by computing the percent errors for each of the predictions. Show your work by using Hypatia Create using the fraction template, writing, for example,

instead of a/b.
Model 1 (n = 1): % error for Plutos’ period = 12.89%

Model 2 (n = 1.5): % error for Plutos’ period = 13.44%

Model 3 (n = 2): % error for Plutos’ period = 13.02% (280.85-248.5/ 248.5 )*100
Task 6:
Write one to two paragraphs in which you rank the models, indicating which is the best model, the second best and the worst one. Support your ranking by using the graph from Task 3, the % errors from Task 4, and the SSE computations from Task 5..
The best model would be Model 1, the second best model would be Model 3 and the lastly, the third best model would be Model 2.
D. Finding a Best Power Model
The three models considered above, even though you may have labeled them as linear, power and quadratic, respectively, are all part of the power model family, since each one consists of just a single power term, not a sum of power terms. The question arises whether there is a power model different from the ones we explored in parts B and C that might fit even better. That is, we will explore different possible value of n.
Task 7:
Use Desmos or Google sheets to fit a power function of the form P=k∙Dn, where both k and n are parameters. If you use Desmos, make sure you use the default names for the variables in Desmos (the ones at the top of the data table) and the ~ for the model fit.
What is the model equation for the parameters that you found in either Desmos or Google sheets? Paste a screenshot of your work that shows the fit and write the answer.
PD=
Are you surprised by the answer? Explain why or why not.
Task 8:
Write a short (2 paragraph) summary of this exploration that would give a classmate who did not yet do the exploration a good overview. You may use the headings of the parts as guidance to explain the big picture. Make sure to state a conclusion.