Please answer #2 and #3 only with the same format as the examples given. Thank you.
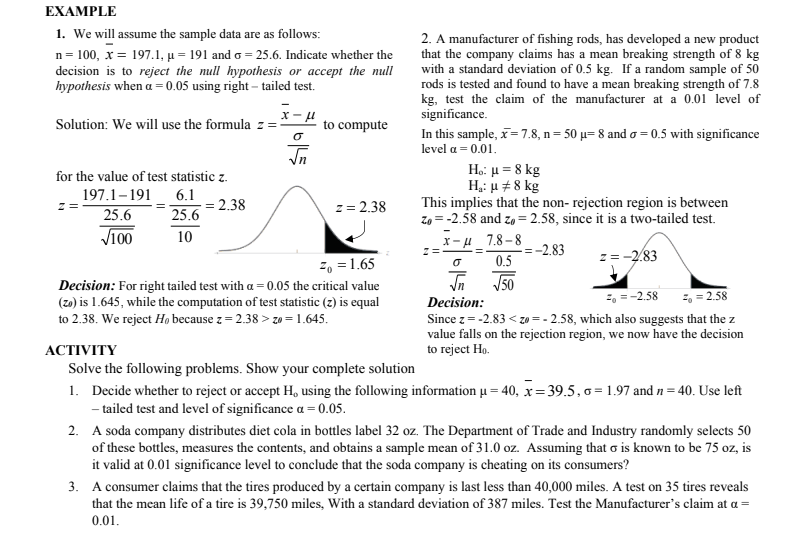
Extracted text: EXAMPLE 1. We will assume the sample data are as follows: n = 100, x = 197.1, µ = 191 and o = 25.6. Indicate whether the decision is to reject the null hypothesis or accept the null hypothesis when a = 0.05 using right – tailed test. 2. A manufacturer of fishing rods, has developed a new product that the company claims has a mean breaking strength of 8 kg with a standard deviation of 0.5 kg. If a random sample of 50 rods is tested and found to have a mean breaking strength of 7.8 kg, test the claim of the manufacturer at a 0.01 level of significance. Solution: We will use the formula z =: to compute In this sample, x= 7.8, n= 50 µ= 8 and o = 0.5 with significance level a = 0.01. Ho: µ = 8 kg H,: u +8 kg for the value of test statistic z. 197.1-191 6.1 This implies that the non- rejection region is between Zo = -2.58 and zo = 2.58, since it is a two-tailed test. 2.38 z= 2.38 z = 25.6 25.6 V100 10 X-u 7.8-8 -2.83 2, = 1.65 0.5 z= -2.83 J50 Decision: For right tailed test with a = 0.05 the critical value (zo) is 1.645, while the computation of test statistic (z) is equal to 2.38. We reject Ho because z = 2.38 > zo = 1.645. =, =-2.58 2, = 2.58 Decision: Since z= -2.83 < zo = - 2.58, which also suggests that the z value falls on the rejection region, we now have the decision to reject ho. аctivity solve the following problems. show your complete solution 1. decide whether to reject or accept h, using the following information µ = 40, x= 39.5, 6 = 1.97 and n = 40. use left - tailed test and level of significance a = 0.05. 2. a soda company distributes diet cola in bottles label 32 oz. the department of trade and industry randomly selects 50 of these bottles, measures the contents, and obtains a sample mean of 31.0 oz. assuming that o is known to be 75 oz, is it valid at 0.01 significance level to conclude that the soda company is cheating on its consumers? 3. a consumer claims that the tires produced by a certain company is last less than 40,000 miles. a test on 35 tires reveals that the mean life of a tire is 39,750 miles, with a standard deviation of 387 miles. test the manufacturer's claim at a = 0.01. zo="-" 2.58,="" which="" also="" suggests="" that="" the="" z="" value="" falls="" on="" the="" rejection="" region,="" we="" now="" have="" the="" decision="" to="" reject="" ho.="" аctivity="" solve="" the="" following="" problems.="" show="" your="" complete="" solution="" 1.="" decide="" whether="" to="" reject="" or="" accept="" h,="" using="" the="" following="" information="" µ="40," x="39.5," 6="1.97" and="" n="40." use="" left="" -="" tailed="" test="" and="" level="" of="" significance="" a="0.05." 2.="" a="" soda="" company="" distributes="" diet="" cola="" in="" bottles="" label="" 32="" oz.="" the="" department="" of="" trade="" and="" industry="" randomly="" selects="" 50="" of="" these="" bottles,="" measures="" the="" contents,="" and="" obtains="" a="" sample="" mean="" of="" 31.0="" oz.="" assuming="" that="" o="" is="" known="" to="" be="" 75="" oz,="" is="" it="" valid="" at="" 0.01="" significance="" level="" to="" conclude="" that="" the="" soda="" company="" is="" cheating="" on="" its="" consumers?="" 3.="" a="" consumer="" claims="" that="" the="" tires="" produced="" by="" a="" certain="" company="" is="" last="" less="" than="" 40,000="" miles.="" a="" test="" on="" 35="" tires="" reveals="" that="" the="" mean="" life="" of="" a="" tire="" is="" 39,750="" miles,="" with="" a="" standard="" deviation="" of="" 387="" miles.="" test="" the="" manufacturer's="" claim="" at="" a="">